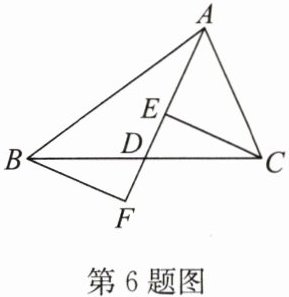
6. 如图,$AD是\triangle ABC$的中线,$E$,$F分别是AD和AD$延长线上的点,且$DE = DF$,连接$BF$,$CE$。给出下列说法:①$CE = BF$;②$\triangle ABD和\triangle ADC$的面积相等;③$BF// CE$;④$AE + AF = 2AD$。其中,正确的个数是(
A
)
A.4
B.3
C.2
D.1
答案:A
解析:
证明:
①
∵AD是△ABC中线,
∴BD=CD。
在△CDE和△BDF中,
$\left\{\begin{array}{l} CD=BD\\ ∠CDE=∠BDF\\ DE=DF\end{array}\right.$
∴△CDE≌△BDF(SAS),
∴CE=BF,①正确。
②
∵AD是中线,
∴BD=CD。
△ABD和△ADC等底同高,
∴$S_{\triangle ABD}=S_{\triangle ADC}$,②正确。
③ 由①知△CDE≌△BDF,
∴∠ECD=∠FBD,
∴BF//CE,③正确。
④
∵AE=AD-DE,AF=AD+DF,且DE=DF,
∴AE+AF=AD-DE+AD+DF=2AD,④正确。
综上,①②③④均正确,正确个数为4。
答案:A
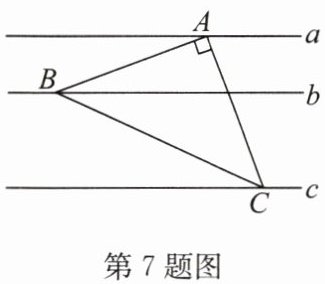
7. 如图,在$\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AB = AC$,三角形的顶点分别在相互平行的三条直线$a$,$b$,$c$上,且$a$,$b$之间的距离为2,$b$,$c$之间的距离为4,则$\triangle ABC$的面积为
20
。
答案:20
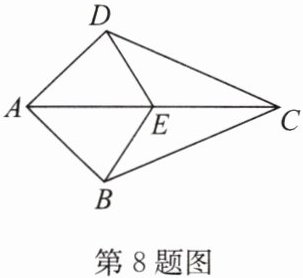
8. 如图,$AB = AD$,$DC = BC$,$E是AC$上的点,连接$DE$,$BE$。求证:$\angle ADE= \angle ABE$。
答案:证明:在△ABC和△ADC中,{AB=AD,
CB=CD,
AC=AC,
∴△ABC≌△ADC(SSS),
∴∠CAB=∠CAD.
在△ADE和△ABE中,{AD=AB,
∠EAD=∠EAB,
AE=AE,
∴△ADE≌△ABE(SAS),
∴∠ADE=∠ABE;
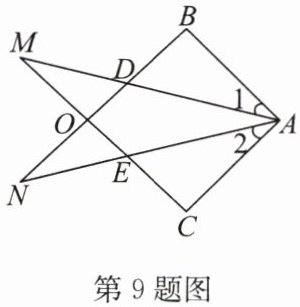
9. $\triangle ABN和\triangle ACM$的位置如图所示,$AB = AC$,$AD = AE$,$\angle 1= \angle 2$。求证:(1)$BD = CE$;(2)$AM = AN$。
答案:证明:
(1)在△ABD和△ACE中,{AB=AC,
∠1=∠2,
AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)
∵∠1=∠2,
∴∠1+∠DAE=∠2+∠DAE,
即∠BAN=∠CAM;
∵△ABD≌△ACE,
∴∠B=∠C;
在△ACM和△ABN中,{∠C=∠B,
AC=AB,
∠CAM=∠BAN,
∴△ACM≌△ABN(ASA),
∴AM=AN.
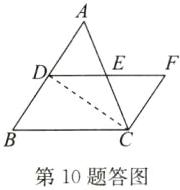
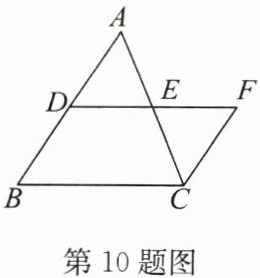
10. (2024·宿豫期中)如图,在$\triangle ABC$中,点$D在AB$上,$E是AC$的中点,$CF// AB$,交$DE的延长线于点F$。
(1)求证:$\triangle AED\cong\triangle CEF$;
(2)若$D是AB$的中点,判断$DE与BC$的关系,并说明理由。
答案:(1)证明:
∵E是AC的中点,
∴AE=CE;
∵CF//AB,
∴∠A=∠FCE,∠ADE=∠F.
在△AED和△CEF中,{∠A=∠FCE,
∠ADE=∠F,
AE=CE,
∴△AED≌△CEF(AAS).
(2)解:DE//BC,DE=$\frac{1}{2}$BC,理由:如答图,连接CD.由
(1)得△AED≌△CEF,
∴AD=CF,DE=FE;
∴DE=$\frac{1}{2}$DF.
∵D是AB的中点,
∴AD=BD.
∴BD=CF.
∵CF//AB,
∴∠BDC=∠FCD.
在△BDC和△FCD中,{BD=FC,
∠BDC=∠FCD,
DC=CD,
∴△BDC≌△FCD(SAS).
∴BC=DF,∠BCD=∠FDC;
∴DE//BC,DE=$\frac{1}{2}$BC.