1. (2024·通州区期末)如图,$CD\perp AB于点D$,$BE\perp AC于点E$,$OB = OC$,则图中全等三角形共有(
C
)
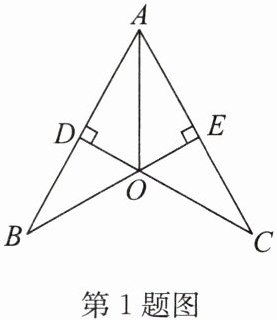
A.2对
B.3对
C.4对
D.5对
答案:C
解析:
证明:
1. 在$\triangle OBD$和$\triangle OCE$中,
$\angle ODB = \angle OEC = 90°$,
$\angle DOB = \angle EOC$,
$OB = OC$,
$\therefore \triangle OBD \cong \triangle OCE(AAS)$,
$\therefore OD = OE$,$BD = CE$;
2. 在$Rt\triangle AOD$和$Rt\triangle AOE$中,
$OA = OA$,
$OD = OE$,
$\therefore Rt\triangle AOD \cong Rt\triangle AOE(HL)$,
$\therefore AD = AE$,$\angle OAD = \angle OAE$;
3. $\because AD = AE$,$BD = CE$,
$\therefore AB = AC$,
在$\triangle AOB$和$\triangle AOC$中,
$AB = AC$,
$\angle OAB = \angle OAC$,
$OA = OA$,
$\therefore \triangle AOB \cong \triangle AOC(SAS)$;
4. 在$\triangle ABE$和$\triangle ACD$中,
$\angle AEB = \angle ADC = 90°$,
$\angle BAE = \angle CAD$,
$AB = AC$,
$\therefore \triangle ABE \cong \triangle ACD(AAS)$。
综上,全等三角形共有4对。
C
2. 如图,要测量河两岸相对的$A$,$B$两点之间的距离,可以在与$AB垂直的河岸BF上取C$,$D$两点,且使$BC = CD$。从点$D出发沿与河岸BF垂直的方向移动到点E$,使点$A$,$C$,$E$在一条直线上。若测量$DE$的长为15米,则$A$,$B$两点之间的距离为
15
米。
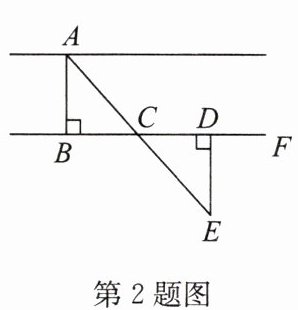
答案:15
解析:
证明:
∵ $AB \perp BF$,$DE \perp BF$,
∴ $\angle ABC = \angle EDC = 90°$。
∵ $\angle ACB = \angle ECD$(对顶角相等),$BC = CD$,
∴ $\triangle ABC \cong \triangle EDC$(ASA)。
∴ $AB = DE$。
∵ $DE = 15$米,
∴ $AB = 15$米。
15
3. 如图,在长方形$ABCD$中,$AB = 4$,$AD = 6$。延长$BC到点E$,使$CE = 2$,连接$DE$,动点$P从点B$出发,以每秒2个单位长度的速度沿$BC - CD - DA向终点A$运动。设点$P的运动时间为t$秒,当$t$为
1或7
时,$\triangle ABP和\triangle DCE$全等。
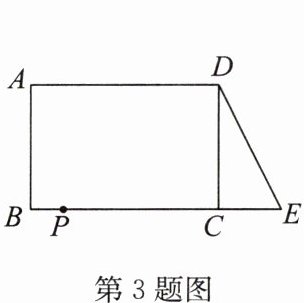
答案:1或7
解析:
解:
$\because$ 四边形$ABCD$是长方形,
$\therefore AB=CD=4$,$AD=BC=6$,$\angle B=\angle DCE=90°$。
$\because CE=2$,$\triangle ABP$和$\triangle DCE$全等,分两种情况:
情况1: $BP=CE=2$,$AB=CD=4$。
$\because P$从$B$出发沿$BC$运动,速度为$2$单位/秒,
$\therefore t=\frac{BP}{2}=\frac{2}{2}=1$。
情况2: $BP=CD=4$,$AB=CE=2$(不成立,$AB=4\neq CE=2$,舍去);或$AP=CE=2$,$AB=CD=4$。
$P$运动路径为$BC-CD-DA$,总路程为$BC+CD+DA=6+4+6=16$。
当$P$在$DA$上时,$AP=2$,则$P$运动路程为$BC+CD+DA-AP=6+4+6-2=14$,
$\therefore t=\frac{14}{2}=7$。
综上,$t=1$或$7$。
答案:$1$或$7$
4. 如图,$AC\perp BC$,$DC\perp EC$,$AC = BC$,$DC = EC$,$AE与BD交于点F$。
(1)求证:$AE = BD$;
(2)求$\angle AFD$的度数。
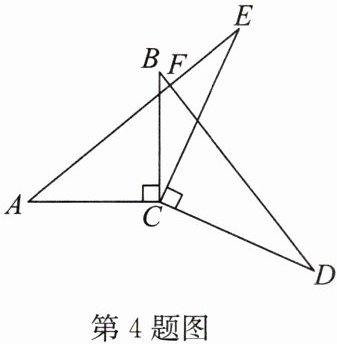
答案:
(1)证明:
∵AC⊥BC,DC⊥EC,
∴∠ACB=∠DCE=90°,
∴∠ACE=∠BCD.
在△ACE和△BCD中,{AC=BC,
∠ACE=∠BCD,
CE=CD,
∴△ACE≌△BCD(SAS),
∴AE=BD.
(2)解:设BC与AE交于点N.
∵∠ACB=90°,
∴∠A+∠ANC=90°.
∵△ACE≌△BCD,
∴∠A=∠B,
∵∠ANC=∠BNF,
∴∠B+∠BNF=90°,
∴∠AFD=∠B+∠BNF=90°.
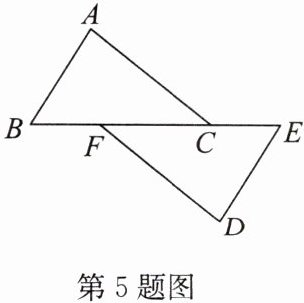
5. (2024·宿豫期中)如图,在$\triangle ABC和\triangle DEF$中,点$B$,$F$,$C$,$E$在同一直线上。已知$AB// DE$,$BF = CE$。给出下列条件:①$\angle A= \angle D$,②$\angle B= \angle E$,③$AC = DF$,④$AC// DF$,能判定$\triangle ABC\cong\triangle DEF$的是(
C
)
A.①②③
B.①②④
C.①④
D.①②③④
答案:C
解析:
证明:
∵ $BF = CE$,
∴ $BF + FC = CE + FC$,即 $BC = EF$。
∵ $AB // DE$,
∴ $\angle B = \angle E$。
条件①:$\angle A = \angle D$,
在$\triangle ABC$和$\triangle DEF$中,
$\begin{cases} \angle A = \angle D \\\angle B = \angle E \\BC = EF \end{cases}$,
∴ $\triangle ABC \cong \triangle DEF$(AAS)。
条件②:$\angle B = \angle E$,
仅一组角和一组边对应相等,无法判定全等。
条件③:$AC = DF$,
SSA无法判定全等。
条件④:$AC // DF$,
∴ $\angle ACB = \angle DFE$,
在$\triangle ABC$和$\triangle DEF$中,
$\begin{cases} \angle B = \angle E \\BC = EF \\\angle ACB = \angle DFE \end{cases}$,
∴ $\triangle ABC \cong \triangle DEF$(ASA)。
综上,能判定全等的是①④。
答案:C