1. 甲、乙、丙 3 人随意排成一排拍照,甲恰好排在中间的概率是
$\frac{1}{3}$
.
答案:$\frac{1}{3}$(或对应的选择题选项字母如题目为选择题形式)
解析:
三人随意排成一排拍照的所有可能排列有 $3! = 6$(种)。
甲恰好排在中间的情况有固定甲在中间位置,其余两人任意排列,即 $2! = 2$(种)排列方式。
所以甲恰好排在中间的概率为 $\frac{2}{6} = \frac{1}{3}$。
2. 从 4 根长度分别是 2 cm,3 cm,4 cm,5 cm 的小木棒中任取 3 根,能搭成三角形的概率是 (
C
)
A.$\frac{1}{4}$
B.$\frac{1}{2}$
C.$\frac{3}{4}$
D.1
答案:C
解析:
从4根小木棒中任取3根,共有以下4种情况:
1. 2 cm, 3 cm, 4 cm:满足三角形条件(2+3>4, 2+4>3, 3+4>2),能搭成三角形。
2. 2 cm, 3 cm, 5 cm:不满足三角形条件(2+3=5,不满足两边之和大于第三边),不能搭成三角形。
3. 2 cm, 4 cm, 5 cm:满足三角形条件(2+4>5, 2+5>4, 4+5>2),能搭成三角形。
4. 3 cm, 4 cm, 5 cm:满足三角形条件(3+4>5, 3+5>4, 4+5>3),能搭成三角形。
共有4种等可能情况,其中能搭成三角形的有3种,因此概率为$\frac{3}{4}$。
3. 4 张扑克牌的点数分别是 2、3、4、8,将它们洗匀后背面朝上放在桌面上.
(1) 从中任意抽取 1 张,求抽到的牌的点数是偶数的概率;
(2) 从中先任意抽取 1 张,再从余下的牌中任意抽取 1 张,求抽到的两张牌的点数都是偶数的概率.
答案:(1)
总共有$4$张牌,点数为偶数的牌有$2$,$4$,$8$共$3$张。
设“抽到的牌的点数为偶数”为事件$A$,根据概率公式$P(A)=\frac{m}{n}$(其中$n$是基本事件总数,$m$是事件$A$所包含的基本事件数),可得$P(A)=\frac{3}{4}$。
(2)
从$4$张牌中先抽一张,再从余下$3$张中抽一张的总可能情况数$n = 4×3=12$种。
要抽到的两张牌的点数都是偶数,第一次抽有$3$种可能(点数为$2$,$4$,$8$的牌),第二次抽有$2$种可能,所以抽到的两张牌的点数都是偶数的情况数$m = 3×2 = 6$种。
设“抽到的两张牌的点数都是偶数”为事件$B$,根据概率公式$P(B)=\frac{m}{n}$,可得$P(B)=\frac{6}{12}=\frac{1}{2}$。
综上,(1)的答案是$\frac{3}{4}$;(2)的答案是$\frac{1}{2}$。
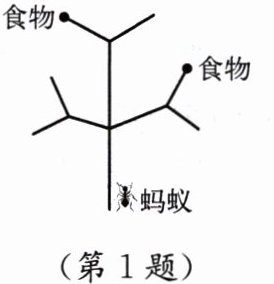
1. 一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都可以随机选择一条路径,并且选择每条路径的可能性相等,则它获得食物的概率是
2/3
.
答案:2/3
解析:
蚂蚁从起点出发,第一个岔路口有3条路径。第一条路径末端无食物;第二条路径末端有1个食物;第三条路径末端有1个食物。总路径数为3,有食物的路径数为2,概率为2/3。
2. 从甲、乙、丙、丁 4 名学生中选 2 名学生进行一次羽毛球单打比赛,求下列事件发生的概率.
(1) 已确定甲参加比赛,再从其余 3 名学生中任意选取 1 名,恰好选中乙;
(2) 任意选取 2 名学生,其中有乙.
答案:(1) 已确定甲参加比赛,从乙、丙、丁3名学生中选1名,共有3种等可能结果,其中选中乙的结果有1种,所以概率为$\frac{1}{3}$。
(2) 从4名学生中任意选取2名,所有可能的结果为:(甲,乙)、(甲,丙)、(甲,丁)、(乙,丙)、(乙,丁)、(丙,丁),共6种等可能结果。其中有乙的结果为:(甲,乙)、(乙,丙)、(乙,丁),共3种,所以概率为$\frac{3}{6}=\frac{1}{2}$。
(1)$\frac{1}{3}$;(2)$\frac{1}{2}$
3. 在如图的方格纸中,点 A、B、C、D、E、F 分别位于小正方形的顶点上.
(1) 从点 A、D、E、F 中任意取一点,以所取的这一点及 B、C 为顶点画三角形,则所画三角形是等腰三角形的概率是
$\frac{1}{2}$
;
(2) 从点 A、D、E、F 中先后任意取两个不同的点,以所取的这两点及 B、C 为顶点画四边形,求所画四边形是平行四边形的概率.
$\frac{1}{3}$

答案:(1) 从点A、D、E、F中任取一点,与B、C构成三角形,共有4种等可能情况。
取A:AB=BC,△ABC是等腰三角形;
取D:DB=DC,△DBC是等腰三角形;
取E:三边不等,不是等腰三角形;
取F:三边不等,不是等腰三角形。
等腰三角形的情况有2种,概率为$\frac{2}{4}=\frac{1}{2}$。
(2) 从A、D、E、F中先后取两个不同点,共有$4×3=12$种等可能结果(有序)。
构成平行四边形需满足对边平行且相等或对角线互相平分,符合条件的组合(无序)为{A,D}、{E,F},对应有序结果4种:(A,D),(D,A),(E,F),(F,E)。
概率为$\frac{4}{12}=\frac{1}{3}$。
(1)$\frac{1}{2}$;(2)$\frac{1}{3}$
4. 一项“闯关游戏”规定:在闯第 n 关时要将一枚质地均匀的骰子抛掷 n 次. 若 n 次抛掷所出现的点数之和大于 $\frac{5}{4}n^{2}$,则为过关;否则为不过关. 第二关过关的概率是 (
A
)
A.$\frac{13}{18}$
B.$\frac{5}{18}$
C.$\frac{1}{4}$
D.$\frac{1}{9}$
答案:A
解析:
第二关需抛掷2次骰子,过关条件为点数之和大于$\frac{5}{4}×2^2 = 5$。
总结果数:$6×6=36$种。
点数之和小于等于5的情况:
$a=1$时,$b=1,2,3,4$(4种);
$a=2$时,$b=1,2,3$(3种);
$a=3$时,$b=1,2$(2种);
$a=4$时,$b=1$(1种);
共$4+3+2+1=10$种。
点数之和大于5的情况数:$36-10=26$种。
概率:$\frac{26}{36}=\frac{13}{18}$。