7.如图,$\odot O$半径为1,$AB是\odot O$的直径,$C是\odot O$上一点,连接$AC$,$\odot O外的一点D在直线AB$上.
(1)已知$AC = \sqrt{3}$,$OB = BD$.
①求证:$CD是\odot O$的切线;
②阴影部分的面积是______
π/3
.(结果保留$\pi$)
(2)当点$C在\odot O$上运动时,若$CD是\odot O$的切线,探究$\angle CDO与\angle OAC$的数量关系.
∠CDO=90°-2∠OAC
(第7题)
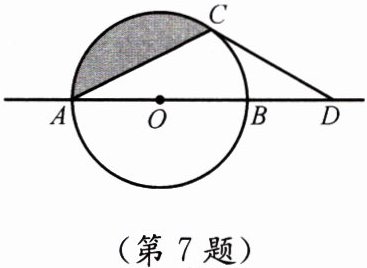
答案:(1)①证明:
连接OC,BC。
∵AB是⊙O直径,∴∠ACB=90°(直径所对圆周角是直角)。
在Rt△ACB中,AB=2(半径为1,直径AB=2),AC=√3,
∴BC=√(AB²-AC²)=√(2²-(√3)²)=1。
∵OB=OC=1(⊙O半径),BC=1,
∴OB=OC=BC,△OBC是等边三角形,∠COB=60°。
∵OB=BD,OB=1,∴BD=1,OD=OB+BD=2。
在△OCD中,OC=1,OD=2,∠COD=60°,
∴CD²=OC²+OD²-2·OC·OD·cos∠COD=1²+2²-2×1×2×cos60°=1+4-2=3,
∴OC²+CD²=1+3=4=OD²,△OCD是直角三角形,∠OCD=90°,即OC⊥CD。
∵OC是⊙O半径,∴CD是⊙O的切线。
②π/3
(2)∠CDO=90°-2∠OAC。
1.如图,点$A$、$B$、$C$、$D是一个外角为40^{\circ}$的正多边形的顶点,若$O$为正多边形的中心,则$\angle OAD$的度数为
30°
.
(第1题)(第2题)

答案:30°
解析:
∵正多边形外角为40°,∴边数n=360°÷40°=9。
∵O为中心,∴OA=OD(半径),∠AOD为A、D对应的中心角。
A、B、C、D为连续顶点,∴A到D相隔3个中心角,∠AOD=3×(360°÷9)=120°。
在△OAD中,OA=OD,∠OAD=(180°-∠AOD)/2=(180°-120°)/2=30°。
2.如图,$\odot M$的半径为2,圆心$M的坐标为(3,4)$,$P是\odot M$上的任意一点,$PA\perp PB$,且$PA$、$PB与x轴分别交于A$、$B$两点,若点$A$、点$B关于原点O$对称,则$AB$的最小值为______
6
.

答案:6
解析:
设点$A(-a,0)$,$B(a,0)$,则$AB=2a$,需求$a$的最小值。设$P(x,y)$,因$PA\perp PB$,向量$\overrightarrow{PA}=(-x-a,-y)$,$\overrightarrow{PB}=(a-x,-y)$,由$\overrightarrow{PA}\cdot\overrightarrow{PB}=0$得$x^2+y^2=a^2$,故点$P$在以$O$为圆心、$a$为半径的圆上。又$P$在$\odot M$上,$\odot M$圆心$(3,4)$,半径$2$,$OM=5$。两圆有公共点,则$|a-2|\leq5\leq a+2$,解得$a\geq3$。当$a=3$时,两圆外切,$a$最小,$AB=2a=6$。
3.如图,在$Rt\triangle ABC$中,$\angle BCA = 90^{\circ}$,$\angle BAC的平分线交\triangle ABC外接圆于点D$,连接$BD$,已知$AB = 2AC = 4$.
(1)求$BD$的长;
(2)设点$P在\overset{\frown}{CAB}上由点C向点B$移动,但不与点$C$、$B$重合,记$\angle PBC的平分线与PD的交点为I$,求点$I随点P的移动所经过的路径长l$的取值范围.
(第3题)

答案:(1) 在$Rt\triangle ABC$中,$\angle BCA=90^\circ$,$AB=4$,$AC=2$,则$BC=\sqrt{AB^2-AC^2}=\sqrt{16-4}=2\sqrt{3}$。$\angle BAC=60^\circ$,$AD$平分$\angle BAC$,则$\angle BAD=30^\circ$。
$AB$为外接圆直径,$\angle ADB=90^\circ$(直径所对圆周角)。在$Rt\triangle ABD$中,$BD=AB\cdot\sin\angle BAD=4\cdot\sin30^\circ=2$。
(2) 由(1)知$AB=4$,外接圆半径为$2$,圆心$O$为$AB$中点。$CD$为直径($CD=4$),$BD\perp BC$(直径所对圆周角为直角)。
点$I$为$\angle PBC$平分线与$PD$交点,可证$I$在以$B$为圆心,$2\sqrt{2}$为半径的圆上。轨迹为圆心角$90^\circ$的圆弧。
弧长$l=\frac{90^\circ}{360^\circ}×2\pi×2\sqrt{2}=\sqrt{2}\pi$。
(1) $BD=2$;(2) $l=\sqrt{2}\pi$
答案
(1) $\boxed{2}$
(2) $\boxed{\sqrt{2}\pi}$
解析:
(1) 在$Rt\triangle ABC$中,$\angle BCA=90^\circ$,$AB=4$,$AC=2$,则$BC=\sqrt{AB^2-AC^2}=\sqrt{4^2-2^2}=2\sqrt{3}$,$\angle BAC=60^\circ$。
因为$AD$平分$\angle BAC$,所以$\angle BAD=30^\circ$。
$\triangle ABC$外接圆中,$AB$为直径,$\angle ADB=90^\circ$。
在$Rt\triangle ABD$中,$BD=AB\cdot\sin\angle BAD=4×\sin30^\circ=4×\frac{1}{2}=2$。
(2) 点$I$的轨迹是以$BD$为弦,圆心角为$120^\circ$的圆弧(不含端点)。
$BD=2$,设圆心为$O$,则$\triangle OBD$为等边三角形,半径$OB=BD=2$。
弧长$l=\frac{120^\circ}{360^\circ}×2\pi×2=\frac{4\pi}{3}$。
因为点$P$不与$C$、$B$重合,所以$0<l<\frac{4\pi}{3}$。
(1)$2$;
(2)$0<l<\frac{4\pi}{3}$