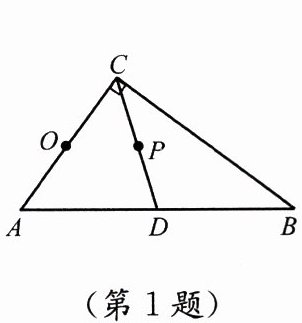
1.如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = 6$,$AB = 10$,$CD是斜边AB$上的中线,以$AC为直径画\odot O$,设线段$CD的中点为P$,则点$P与\odot O$的位置关系是 (
A
)
A.点$P在\odot O$内
B.点$P在\odot O$上
C.点$P在\odot O$外
D.无法确定
(第1题)(第2题)
答案:A
解析:
在$Rt\triangle ABC$中,$\angle ACB=90^\circ$,$AC=6$,$AB=10$,由勾股定理得$BC=\sqrt{AB^2-AC^2}=\sqrt{10^2-6^2}=8$。
$CD$是斜边$AB$上的中线,故$CD=\frac{1}{2}AB=5$,$P$为$CD$中点,则$CP=\frac{5}{2}=2.5$。
以$AC$为直径画$\odot O$,圆心$O$为$AC$中点,半径$r=\frac{AC}{2}=3$。
建立坐标系:设$C(0,0)$,$A(0,6)$,$B(8,0)$,则$AB$中点$D$坐标为$(\frac{0+8}{2},\frac{6+0}{2})=(4,3)$。
$CD$中点$P$坐标为$(\frac{0+4}{2},\frac{0+3}{2})=(2,1.5)$,圆心$O$坐标为$(\frac{0+0}{2},\frac{6+0}{2})=(0,3)$。
计算$OP$距离:$OP=\sqrt{(2-0)^2+(1.5-3)^2}=\sqrt{4+2.25}=\sqrt{6.25}=2.5$。
$\odot O$半径$r=3$,因$OP=2.5\lt3$,故点$P$在$\odot O$内。
2.如图,$AB为\odot O$的直径,点$C$、$D在\odot O$上,$\angle BAC = 50^{\circ}$,则$\angle ADC = $
$40^{\circ}$
.

答案:$40^{\circ}$(由于要求只填结果相关内容,这里若按填空题形式本应填$40^{\circ}$ ,若题目是选择题形式才填选项,本题按非选择题解析,若强制按答案格式要求,可理解为填$40$ (度数数值) )
解析:
连接$BC$。
因为$AB$是$\odot O$的直径,根据直径所对的圆周角是直角,
所以$\angle ACB = 90^{\circ}$。
已知$\angle BAC = 50^{\circ}$,在$\triangle ABC$中,根据三角形内角和为$180^{\circ}$,
可得$\angle ABC=180^{\circ}-\angle ACB - \angle BAC=180^{\circ}-90^{\circ}-50^{\circ}=40^{\circ}$。
因为同弧所对的圆周角相等,$\angle ADC$和$\angle ABC$都是弧$AC$所对的圆周角,
所以$\angle ADC=\angle ABC = 40^{\circ}$。
3.如图,半径为5的$\odot P与y轴交于点M(0,-4)$、$N(0,-10)$,则点$P$的坐标为
$(-4,-7)$
.
(第3题)(第5题)

答案:$(-4,-7)$
解析:
设点$P$的坐标为$(x,y)$,因为$\odot P$与$y$轴交于$M(0,-4)$、$N(0,-10)$,所以$PM=PN=5$。
$M$、$N$在$y$轴上,两点间距离为$\vert -4 - (-10)\vert = 6$,则$MN$中点坐标为$(0, \frac{-4 + (-10)}{2})=(0,-7)$。
$P$在线段$MN$的垂直平分线上,$MN$在$y$轴上,垂直平分线为平行于$x$轴的直线,所以$y=-7$。
$PM=5$,根据勾股定理,$x^2 + [(-7) - (-4)]^2 = 5^2$,即$x^2 + (-3)^2 = 25$,$x^2 = 16$,$x = \pm 4$。由图知$P$在第二象限,$x=-4$,故$P(-4,-7)$。
4.在边长为$6cm$、$5cm$、$5cm$的三角形铁皮上剪下一个最大的圆,此圆的半径为
1.5cm
.
答案:1.5cm
解析:
该三角形为等腰三角形,腰长5cm,底边长6cm。半周长$s=\frac{6+5+5}{2}=8cm$。作底边上的高,由勾股定理得高$h=\sqrt{5^2-3^2}=4cm$,面积$S=\frac{6×4}{2}=12cm^2$。设内切圆半径为$r$,由$S=rs$得$r=\frac{S}{s}=\frac{12}{8}=1.5cm$。
5.如图,在矩形金属框$ABCD$中,已知$AB = 2cm$,$BC = 4cm$,现有一根长为$2cm的木棒EF$紧靠着矩形框(即两个端点始终落在矩形的边上),按逆时针方向滑动1周,则木棒$EF的中点P$的运动轨迹所围成的图形的面积为______
4
$cm^{2}$.

答案:$\boxed{4}$
解析:
解题步骤:
1. 建立坐标系:设矩形 $ABCD$ 中,$B(0,0)$,$C(4,0)$,$D(4,2)$,$A(0,2)$。木棒 $EF=2cm$,中点 $P$ 到 $E$、$F$ 距离均为 $1cm$。
2. 分析滑动阶段:
阶段1:$E$ 在 $AB$,$F$ 在 $BC$,$P$ 轨迹为以 $B(0,0)$ 为圆心、半径 $1$ 的四分之一圆弧($x^2+y^2=1$)。
阶段2:$E$、$F$ 在 $BC$,$P$ 轨迹为线段 $y=0$($x$ 从 $1$ 到 $3$)。
阶段3:$E$ 在 $BC$,$F$ 在 $CD$,$P$ 轨迹为以 $C(4,0)$ 为圆心、半径 $1$ 的四分之一圆弧($(4-x)^2+y^2=1$)。
阶段4:$E$、$F$ 在 $CD$(不可能,$CD=2cm$)。
阶段5:$E$ 在 $CD$,$F$ 在 $DA$,$P$ 轨迹为以 $D(4,2)$ 为圆心、半径 $1$ 的四分之一圆弧($(4-x)^2+(2-y)^2=1$)。
阶段6:$E$、$F$ 在 $DA$,$P$ 轨迹为线段 $y=2$($x$ 从 $3$ 到 $1$)。
阶段7:$E$ 在 $DA$,$F$ 在 $AB$,$P$ 轨迹为以 $A(0,2)$ 为圆心、半径 $1$ 的四分之一圆弧($x^2+(2-y)^2=1$)。
3. 轨迹围成图形:四段圆弧(共一个整圆,面积 $\pi × 1^2 = \pi$)与四段线段围成中间矩形(长 $2$、宽 $2$,面积 $2 × 2 = 4$)。但圆弧在矩形内部抵消,实际围成图形为矩形。
结论:
中点 $P$ 的运动轨迹所围成的图形面积为 $4$。
6.某体育中心要修建一座公共服务设施,使它到三所运动员公寓$A$、$B$、$C$的距离相等.
(1)若三所运动员公寓$A$、$B$、$C$的位置如图所示,请你在图中确定该公共服务设施(用点$P$表示)的位置;
(2)若$\angle BAC = 66^{\circ}$,求$\angle BPC$.
$A\bullet$
$\bullet C$
$B\bullet$
(第6题)

答案:(1) 如图所示(作图痕迹为AB、AC的垂直平分线,交点P);(2) 132°。
解析:
(1) 分别作线段AB、AC的垂直平分线,两垂直平分线交于点P,点P即为所求。
(2) ∵点P是△ABC的外心,∴PA=PB=PC,∠BPC=2∠BAC。
∵∠BAC=66°,∴∠BPC=2×66°=132°。