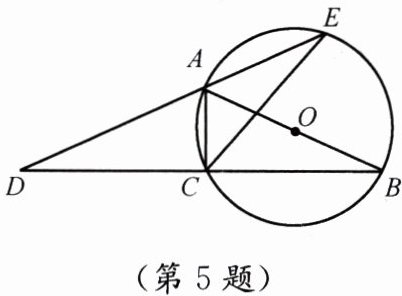
5. 如图,AB 为⊙O 的直径,点 C 在⊙O 上,延长 BC 到点 D,使 DC = CB,延长 DA,交⊙O 于点 E,连接 AC、CE。
(1)试说明∠B = ∠D;
(2)若 AB = 4,BC - AC = 2,求 CE 的长。
解析:
(1)∵AB是⊙O直径,∴∠ACB=90°(直径所对圆周角是直角)。
∵D在BC延长线上,∴∠ACD=180°-∠ACB=90°。
∵DC=CB,∠ACD=∠ACB=90°,AC=AC,
∴△ACD≌△ACB(SAS),∴∠D=∠B。
(2)设AC=x,BC=y,∵BC-AC=2,∴y=x+2。
∵AB是直径,AB=4,∴∠ACB=90°,∴AC²+BC²=AB²,即x²+y²=16。
将y=x+2代入x²+y²=16,得x²+(x+2)²=16,
整理得2x²+4x-12=0,即x²+2x-6=0,
解得x=-1±√7,∵x>0,∴x=√7-1,
∴y=x+2=√7+1,即BC=√7+1。
∵∠B=∠D(已证),∠B=∠AEC(同弧AC所对圆周角相等),
∴∠D=∠AEC=∠DEC,∴CE=CD。
∵DC=CB,∴CE=CB=√7+1。