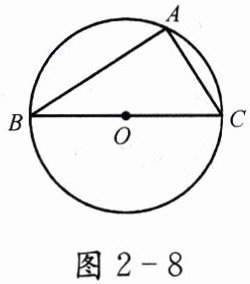
1. 如图 2 - 8,BC 是⊙O 的直径,A 是⊙O 上任意一点,求出∠BAC 的度数。
答案:答题
∵ BC 是⊙O 的直径,
∴ ∠BAC = 90°(直径所对的圆周角是直角)。
2. 如图 2 - 9,点 A 在⊙O 上,∠BAC = 90°,弦 BC 经过圆心吗?为什么?

答案:BC 经过圆心 O。
理由如下:
连接 OA。
因为$\angle BAC = 90^{\circ}$,
所以$\angle BAO+\angle OAC = 90^{\circ}$。
因为 OA = OB = OC(同圆的半径相等),
所以$\angle B=\angle BAO$,$\angle C=\angle OAC$。
所以$\angle B+\angle C+\angle BAC=\angle BAO+\angle OAC + 90^{\circ}=180^{\circ}$(三角形内角和为$180^{\circ}$)。
即$\angle B+\angle C = 90^{\circ}$,把$\angle B=\angle BAO$,$\angle C=\angle OAC$代入可得$\angle BAO+\angle OAC+90^{\circ}=180^{\circ}$中的$\angle BAO+\angle OAC = 90^{\circ}$,那么$\angle AOB+\angle AOC = 180^{\circ}$($\angle AOB = 2\angle B$的邻补角相关推导,根据圆周角相关性质,这里可通过三角形内角关系及等腰三角形性质得出$\angle AOB = 2\angle C$,$\angle AOC = 2\angle B$,所以$\angle AOB+\angle AOC=2(\angle B + \angle C)=180^{\circ}$)。
所以$\angle BOC = 180^{\circ}$,即 B、O、C 三点共线。
所以弦 BC 经过圆心。
3. 归纳发现:
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等;半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
。
答案:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等;半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
解析:
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等;半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
1. 在活动一的问题 1 中添加条件“∠B = 20°”,求∠C 以及$\overset{\frown}{AC}$的度数。
答案:答案略
解析:
由于题目中未给出活动一问题1的原始图形及相关条件(如是否为圆内接三角形、等腰三角形等),仅添加“∠B = 20°”无法确定∠C和$\overset{\frown}{AC}$的度数,因此无法完成作答。1
2. 如图 2 - 10,在⊙O 中,直径 AB 的长为 10 cm,弦 AC 的长为 6 cm,∠ACB 的平分线交⊙O 于点 D,求 BC、AD 和 BD 的长。

答案:答题卡:
1.求$BC$的长:
因为$AB$是$\odot O$的直径,所以$\angle ACB = \angle ADB = 90^{\circ}$(直径所对的圆周角是直角)。
在$Rt\triangle ABC$中,$AB = 10\mathrm{cm}$,$AC = 6\mathrm{cm}$,根据勾股定理$BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{10^{2}-6^{2}} = 8\mathrm{cm}$。
2.求$AD$和$BD$的长:
因为$CD$平分$\angle ACB$,所以$\angle ACD=\angle BCD$,则$\overset{\frown}{AD}=\overset{\frown}{BD}$(在同圆或等圆中,相等的圆周角所对的弧相等),所以$AD = BD$(在同圆或等圆中,相等的弧所对的弦相等)。
在$Rt\triangle ABD$中,$AB = 10\mathrm{cm}$,设$AD = BD = x\mathrm{cm}$,根据勾股定理$AD^{2}+BD^{2}=AB^{2}$,即$2x^{2}=10^{2}$,$x^{2}=50$,解得$x = 5\sqrt{2}\mathrm{cm}$,所以$AD = BD = 5\sqrt{2}\mathrm{cm}$。
综上,$BC$的长为$8\mathrm{cm}$,$AD$和$BD$的长均为$5\sqrt{2}\mathrm{cm}$。
1. 将直角三角尺摆放在下列圆弧上,其中,圆弧恰好为半圆的是(
B
)

答案:B
解析:
根据圆周角定理的推论,半圆(或直径)所对的圆周角是直角。直角三角尺的直角顶点在圆弧上,若圆弧为半圆,则直角的两边应分别经过半圆的两个端点。观察各选项,只有选项B中三角尺的直角顶点在圆弧上,且两条直角边与圆弧分别交于两点,这两点的连线为圆弧的直径,故圆弧为半圆。