1. 思考问题并按照下列要求作图:
(1) 作一个圆需要知道什么条件?
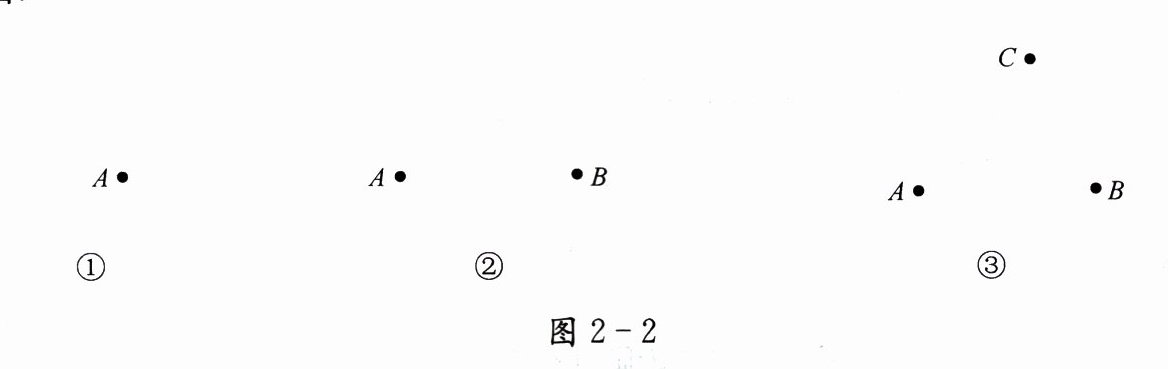
(2) 在图 2 - 2①中,过点 $ A $ 是否可以作圆?如果能,可以作几个?
(3) 在图 2 - 2②中,过 $ A $、$ B $ 两点是否可以作圆?如果能,可以作几个?
(4) 在图 2 - 2③中,过 $ A $、$ B $、$ C $ 三点是否可以作圆?如果能,怎样确定圆心和半径?如果不能,说明理由.
答案:(1) 作一个圆需要知道圆心和半径,或者三个不共线的点。
(2) 可以作无数个圆,因为单一点不能确定圆心和半径,可以以任意点为圆心,以该点到点 $A$ 的距离为半径作圆。
(3) 可以作无数个圆,因为过两点 $A$、$B$ 的圆的圆心必定在这两点的垂直平分线上,半径为圆心到 $A$ 或 $B$ 的距离。
(4)如果 $A$、$B$、$C$ 三点共线,则不能作圆;
如果 $A$、$B$、$C$ 三点不共线,
确定圆心:作 $AB$ 和 $BC$ 的垂直平分线,交点即为圆心 $O$。
确定半径:圆心 $O$ 到 $A$、$B$、$C$ 中任意一点的距离即为半径。
可以作一个圆。
2. 通过上述操作可以得到什么结论?
答案:不在同一直线上的三个点确定一个圆。
1. 如图 2 - 3,观察 $ \odot O $ 与 $ \triangle ABC $ 的关系. 填空:
过三角形的三个顶点可以确定一个圆,这个圆叫做
三角形的外接圆
,______
外接圆
的圆心叫做______
三角形的外心
,该三角形叫做这个圆的______
内接三角形
. 三角形的外心是______
三边垂直平分线
的交点.

答案:三角形的外接圆;外接圆;三角形的外心;内接三角形;三边垂直平分线
解析:
过三角形三个顶点的圆叫三角形的外接圆,外接圆的圆心叫三角形的外心,该三角形叫这个圆的内接三角形,三角形的外心是三边垂直平分线的交点。
2. 如图 2 - 4,$ \triangle ABC $ 分别为锐角三角形、直角三角形、钝角三角形,分别画出它们的外接圆,并指出三角形的外心所在的位置.

答案:答题卡:
1. 锐角三角形 $ABC$ 外接圆及外心:
分别作 $AB$,$BC$ 的垂直平分线,交点为 $O$,以 $O$ 为圆心,$OA$ 长为半径作圆,$\odot O$ 即为 $\triangle ABC$ 的外接圆,外心 $O$ 在三角形内部。
2. 直角三角形 $ABC$ 外接圆及外心:
分别作 $AB$,$AC$ 的垂直平分线,交点为 $O$,以 $O$ 为圆心,$OA$ 长为半径作圆,$\odot O$ 即为 $\triangle ABC$ 的外接圆,外心 $O$ 为斜边 $AC$ 的中点。
3. 钝角三角形 $ABC$ 外接圆及外心:
分别作 $AB$,$BC$ 的垂直平分线,交点为 $O$,以 $O$ 为圆心,$OA$ 长为半径作圆,$\odot O$ 即为 $\triangle ABC$ 的外接圆,外心 $O$ 在三角形外部。