2. 一水平放置的圆柱形输水管道横截面如图所示,管道内水面宽为 $ 0.8 \, m $,最深处水深为 $ 0.2 \, m $,此输水管道的直径是 (
D
)
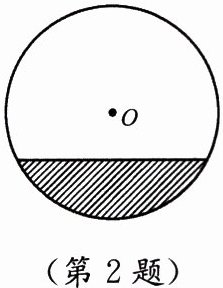
A.$ 0.4 \, m $
B.$ 0.5 \, m $
C.$ 0.8 \, m $
D.$ 1 \, m $
答案:D
解析:
设圆的半径为$r$米,过圆心$O$作弦$AB$(水面宽)的垂线,垂足为$C$,则$AC = \frac{0.8}{2} = 0.4$米。由水深$0.2$米,得圆心到水面距离$OC = r - 0.2$。在$Rt\triangle OAC$中,$OA^2 = AC^2 + OC^2$,即$r^2 = 0.4^2 + (r - 0.2)^2$。解得$r = 0.5$,直径为$2r = 1$米。
3. 如图,在平面直角坐标系 $ xOy $ 中,以点 $ P $ 为圆心,$ 2\sqrt{5} $ 为半径的圆弧交 $ x $ 轴于点 $ A $、$ B $,点 $ A $ 的坐标为 $ (2,0) $,点 $ B $ 的坐标为 $ (6,0) $,则圆心 $ P $ 的坐标为 __
(4,4)
__.

答案:(4,4)
解析:
过点P作PC⊥AB于点C,连接PA。
∵A(2,0),B(6,0),∴AB=4,AC=BC=2,OC=OA+AC=4,∴点C坐标为(4,0)。
设P(4,y),PA=2√5,AC=2,在Rt△PAC中,由勾股定理得:2²+y²=(2√5)²,解得y=±4。
由图知点P在x轴上方,∴y=4,故P(4,4)。
4. 如图,以点 $ O $ 为圆心的两个同心圆中,大圆的弦 $ AB $ 交小圆于 $ C $、$ D $ 两点,且 $ AC = 2 $,求 $ BD $ 的长.

答案:过点 $ O $ 作 $ OE \perp AB $ 于点 $ E $.
因为 $ OE \perp AB $,由垂径定理得:
$ AE = BE $,$ CE = DE $.
所以 $ AE - CE = BE - DE $,即 $ AC = BD $.
因为 $ AC = 2 $,所以 $ BD = 2 $.
答案:2
1. $ \odot O $ 的半径为 5,弦 $ AB // CD $,$ AB = 6 $,$ CD = 8 $,则 $ AB $ 与 $ CD $ 间的距离为 (
C
)
A.1
B.7
C.1 或 7
D.3 或 4
答案:C
解析:
1. 作$OE \perp AB$于$E$,交$CD$于$F$,连$OA,OC$。由垂径定理,$AE = \frac{AB}{2} = 3$,$CF = \frac{CD}{2} = 4$。
2. 在$\triangle OAE$中,$OA = 5$,由勾股定理得$OE = \sqrt{5^2 - 3^2} = 4$。
3. 在$\triangle OCF$中,$OC = 5$,由勾股定理得$OF = \sqrt{5^2 - 4^2} = 3$。
4. 分两种情况讨论:
当$AB,CD$在圆心同侧时,距离为$|OE - OF| = |4 - 3| = 1$;
当$AB,CD$在圆心两侧时,距离为$OE + OF = 4 + 3 = 7$。
综上,距离为$1$或$7$,选C。
2. 已知 $ P $ 为 $ \odot O $ 内一点,过点 $ P $ 的弦中,最长的弦长为 $ 10 \, cm $,最短的弦长为 $ 8 \, cm $,则 $ OP = $
3 cm
.
答案:$3 cm$(或 填数值3 )
解析:
设圆的半径为 $R$,过点 $P$ 的最长弦为直径,所以 $2R = 10$,即 $R = 5(cm)$。
过点 $P$ 的最短弦是与过点 $P$ 的直径垂直的弦,设该弦为 $AB$,且 $AB = 8(cm)$,由于 $AB$ 是垂直于过 $P$ 的直径的弦,根据垂径定理可得:
$AP = \frac{AB}{2} = 4 (cm)$,
在直角三角形 $AOP$ 中,利用勾股定理,有:
$OP = \sqrt{R^{2} - AP^{2}} = \sqrt{5^{2} - 4^{2}} = \sqrt{25 - 16} = \sqrt{9} = 3(cm)$。
3. 如图,在 $ \odot O $ 中,直径 $ AB = 6 $,$ BC $ 是弦,$ \angle ABC = 30^{\circ} $,点 $ P $ 在弦 $ BC $ 上运动,点 $ Q $ 在 $ \odot O $ 上运动,且保持 $ OP \perp PQ $.
(1) 当 $ PQ // AB $ 时,求 $ PQ $ 的长;
(2) 求 $ PQ $ 的长的最大值.

答案:(1) 连接OQ,∵AB是直径,∴∠ACB=90°。在Rt△ABC中,AB=6,∠ABC=30°,∴BC=AB·cos30°=6×(√3/2)=3√3。直线BC方程:由B(3,0),C(-3/2, 3√3/2)得斜率k=-√3/3,方程为y=-√3/3 x+√3。
∵PQ//AB,AB为x轴,PQ斜率为0,OP⊥PQ,∴OP斜率不存在,即P横坐标为0。代入BC方程得P(0,√3),OP=√(0²+(√3)²)=√3。
∵OP⊥PQ,OQ=3,∴在Rt△OPQ中,PQ=√(OQ²-OP²)=√(9-3)=√6。
(2) ∵OP⊥PQ,∴PQ=√(OQ²-OP²)=√(9-OP²)。要使PQ最大,需OP最小。OP最小值为O到BC的距离d。直线BC:√3 x+3y-3√3=0,d=|0+0-3√3|/√( (√3)²+3² )=3√3/√12=3/2。
∴PQ最大值=√(9-(3/2)²)=√(27/4)=3√3/2。
(1) √6;(2) 3√3/2。