18. (10分)甲、乙、丙、丁4位同学进行一次乒乓球单打比赛,要从中选出2位同学打第一场比赛.
(1)请用画树状图或列表的方法,求恰好选中甲、乙2位同学的概率;
(2)若已确定甲打第一场,再从其余3位同学中随机选取1位,求恰好选中乙同学的概率.
答案:(1)
列表法:
| | 甲 | 乙 | 丙 | 丁 |
| --- | --- | --- | --- | --- |
| 甲 | - | (甲,乙) | (甲,丙) | (甲,丁) |
| 乙 | (乙,甲) | - | (乙,丙) | (乙,丁) |
| 丙 | (丙,甲) | (丙,乙) | - | (丙,丁) |
| 丁 | (丁,甲) | (丁,乙) | (丁,丙) | - |
所有可能的情况数有$12$种,其中恰好选中甲、乙两位同学的情况数有$2$种。
$P(恰好选中甲、乙)=\frac{2}{12}=\frac{1}{6}$
(2)
已确定甲打第一场,从其余$3$位同学中随机选取$1$位,总共有$3$种等可能结果,恰好选中乙同学的情况有$1$种。
$P(恰好选中乙)=\frac{1}{3}$
综上,(1)中概率为$\frac{1}{6}$;(2)中概率为$\frac{1}{3}$。
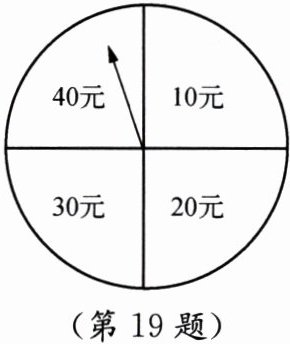
19. (10分)端午节期间,某商场为了吸引顾客,开展有奖促销活动. 如图,转盘被分成4个面积相等的扇形,4个扇形区域里分别标有“10元”“20元”“30元”“40元”的字样. 促销活动规定:同一日内,顾客在本商场每消费满100元就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券. 某顾客当天消费240元,转了两次转盘.
(1)该顾客最少可得
20
元购物券,最多可得______
80
元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.
答案:(1) 20;80
(2) 列表如下:
| 第二次\第一次 | 10 | 20 | 30 | 40 |
|--------------|------|------|------|------|
| 10 | 20 | 30 | 40 | 50 |
| 20 | 30 | 40 | 50 | 60 |
| 30 | 40 | 50 | 60 | 70 |
| 40 | 50 | 60 | 70 | 80 |
共有16种等可能结果,其中金额不低于50元的结果有10种,
∴ P(不低于50元)=10/16=5/8.