10. 已知数据1,2,1,0,$-1$,$-2$,0,$-1$,这组数据的方差是
$\frac{3}{2}$(或 1.5)
.
答案:$\frac{3}{2}$(或 1.5)
解析:
先求这组数据的平均数,$\bar{x}=\frac{1 + 2+1+0 - 1-2+0 - 1}{8}=0$。
再根据方差公式$s^{2}=\frac{1}{n}[(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+\cdots+(x_{n}-\bar{x})^{2}]$,可得$s^{2}=\frac{1}{8}[(1 - 0)^{2}+(2 - 0)^{2}+(1 - 0)^{2}+(0 - 0)^{2}+(-1 - 0)^{2}+(-2 - 0)^{2}+(0 - 0)^{2}+(-1 - 0)^{2}]=\frac{1 + 4+1+0+1+4+0+1}{8}=\frac{12}{8}=\frac{3}{2}$。
11. 已知一组数据$-4$,$x$,4,5,$-5$的平均数是1,那么这组数据的方差是
20.4
.
答案:20.4
解析:
由平均数为1,得$\frac{-4 + x + 4 + 5 - 5}{5} = 1$,解得$x = 5$。数据为$-4$,$5$,$4$,$5$,$-5$。方差$s^2 = \frac{1}{5}[(-4 - 1)^2 + (5 - 1)^2 + (4 - 1)^2 + (5 - 1)^2 + (-5 - 1)^2] = \frac{1}{5}[25 + 16 + 9 + 16 + 36] = \frac{102}{5} = 20.4$
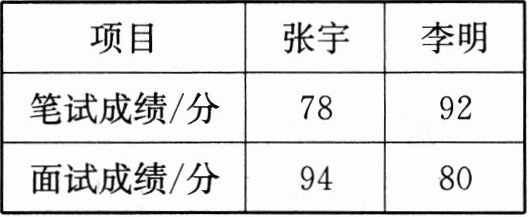
12. 某学校决定招聘一位数学教师,对应聘者进行笔试和面试两项综合考核,其中,笔试成绩占30%,面试成绩占70%,应聘者张宇、李明两人的得分如下表. 你认为
张宇
会被录用.
| 项目 | 张宇 | 李明 |
| 笔试成绩/分 | 78 | 92 |
| 面试成绩/分 | 94 | 80 |
答案:张宇
解析:
根据权重计算张宇的综合成绩:
$综合成绩 = 笔试成绩 × 30\% + 面试成绩 × 70\%$。
张宇:$78 × 0.3 + 94 × 0.7 = 23.4 + 65.8 = 89.2$(分)。
李明:$92 × 0.3 + 80 × 0.7 = 27.6 + 56 = 83.6$(分)。
比较两人的综合成绩,张宇的综合成绩更高,因此张宇会被录用。
13. 已知一组数据$x_{1}$,$x_{2}$,$x_{3}$,$x_{4}$,$x_{5}$的平均数是2,方差是$\frac{1}{3}$,那么数据$3x_{1} - 2$,$3x_{2} - 2$,$3x_{3} - 2$,$3x_{4} - 2$,$3x_{5} - 2$的平均数是
4
,方差是
3
.
答案:4,3
解析:
已知数据$x_{1},x_{2},x_{3},x_{4},x_{5}$的平均数$\overline{x}=2$,方差$s^{2}=\frac{1}{3}$。
新数据$3x_{i}-2$的平均数:$\overline{y}=\frac{1}{5}\sum_{i=1}^{5}(3x_{i}-2)=3×\frac{1}{5}\sum_{i=1}^{5}x_{i}-2=3\overline{x}-2=3×2 - 2=4$。
新数据的方差:$s_{y}^{2}=\frac{1}{5}\sum_{i=1}^{5}(3x_{i}-2 - \overline{y})^{2}=\frac{1}{5}\sum_{i=1}^{5}(3x_{i}-2 - 4)^{2}=\frac{1}{5}\sum_{i=1}^{5}(3x_{i}-6)^{2}=9×\frac{1}{5}\sum_{i=1}^{5}(x_{i}-2)^{2}=9s^{2}=9×\frac{1}{3}=3$。
14. 九年级上学期期末考试后,甲、乙两个班的数学成绩数据的统计情况如下表:

| 班级 | 考试人数 | 平均数 | 中位数 | 众数 | 方差 |
| 甲 | 55 | 88 | 76 | 81 | 108 |
| 乙 | 55 | 85 | 72 | 80 | 112 |
从成绩的波动情况来看,
乙
班学生成绩的波动更大.
答案:乙
解析:
方差是衡量数据波动情况的一个指标,方差越大,表明这组数据波动越大,方差越小,表明这组数据波动越小。甲班方差为$108$,乙班方差为$112$,因为$112>108$,所以乙班学生成绩的波动更大。
15. (10分)某餐饮公司为一工厂提供午餐,分别有8元、10元和15元3种价格的盒饭供员工选择(每人限订1份). 下面是10月份的销售统计图,这个月一共销售了12 500份盒饭,那么员工购买午餐费用的平均数、中位数和众数各是多少?

答案:平均数$9.45$元,中位数$8$元,众数$8$元。
解析:
平均数
8元盒饭销量:$12500 × 65\% = 8125$(份)
10元盒饭销量:$12500 × 20\% = 2500$(份)
15元盒饭销量:$12500 × 15\% = 1875$(份)
总费用:$8 × 8125 + 10 × 2500 + 15 × 1875 = 65000 + 25000 + 28125 = 118125$(元)
平均数:$\frac{118125}{12500} = 9.45$(元)
中位数
总份数排序后第$6250$和$6251$份为中位数位置。
8元盒饭销量$8125 > 6251$,故中位数为$8$元。
众数
8元盒饭销量占比$65\%$最高,故众数为$8$元。