7. 已知 $\odot O$ 的圆心 $O$ 到直线 $l$ 的距离为 $d$,$\odot O$ 的半径为 $r$. 若 $d、r$ 是关于 $x$ 的方程 $x^{2} - 8x + m - 2 = 0$ 的两个实数根,且直线 $l$ 与 $\odot O$ 相切,则 $m = $
18
.
答案:18
解析:
因为直线 $ l $ 与 $ \odot O $ 相切,所以圆心 $ O $ 到直线 $ l $ 的距离 $ d $ 等于半径 $ r $,即 $ d = r $。
由于 $ d $、$ r $ 是方程 $ x^{2} - 8x + m - 2 = 0 $ 的两个实数根,且 $ d = r $,所以该方程有两个相等的实数根。
对于一元二次方程 $ ax^2 + bx + c = 0 $,判别式 $ \Delta = b^2 - 4ac $,当 $ \Delta = 0 $ 时,方程有两个相等的实数根。
在方程 $ x^{2} - 8x + m - 2 = 0 $ 中,$ a = 1 $,$ b = -8 $,$ c = m - 2 $,所以:
$ \Delta = (-8)^2 - 4 × 1 × (m - 2) = 0 $
$ 64 - 4(m - 2) = 0 $
$ 64 - 4m + 8 = 0 $
$ 72 - 4m = 0 $
$ 4m = 72 $
$ m = 18 $
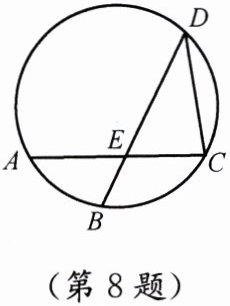
8. 如图,弦 $AC、BD$ 相交于点 $E$,且 $\overset{\frown}{AB} = \overset{\frown}{BC} = \overset{\frown}{CD}$,$\angle BEC = 110^{\circ}$,则 $\angle ACD$ 的度数是
75°
.
答案:75°
解析:
设弧AB=弧BC=弧CD=x,∠ACD=y。
∵∠BEC是△ECD的外角,∴∠BEC=∠EDC+∠ECD。
∠EDC=∠BDC(圆周角),所对弧BC,故∠EDC= x/2;∠ECD=y,∴x/2 + y=110°①。
∠ACD=y为圆周角,所对弧AD,故弧AD=2y。
∵整个圆周长为360°,∴弧AB+弧BC+弧CD+弧AD=3x+2y=360°②。
联立①②:由①得y=110°-x/2,代入②得3x+2(110°-x/2)=360°,解得x=70°。
∴y=110°-70°/2=75°,即∠ACD=75°。
9. 已知 $\triangle ABC$ 的周长为 14 cm,面积为 $7\ cm^{2}$,则 $\triangle ABC$ 的内切圆半径为
1
cm.
答案:1
解析:
设△ABC的内切圆半径为r cm,周长为C=14 cm,面积为S=7 cm²。根据三角形面积与内切圆半径的关系S=½Cr,可得7=½×14×r,解得r=1。
10. 已知 $\angle AOB = 30^{\circ}$,$M$ 为 $OB$ 上的一点,以点 $M$ 为圆心,2 cm 为半径作 $\odot M$ 与 $OA$ 相切,切点为 $N$,则 $\triangle MON$ 的面积为______
2√3
.
答案:2√3
解析:
连接MN,因为OA与⊙M相切于N,所以MN⊥OA,MN=2cm。在Rt△MON中,∠AOB=30°,∠ONM=90°,所以MN=1/2 OM,即OM=4cm。由勾股定理得ON=√(OM²-MN²)=√(4²-2²)=2√3 cm。则△MON面积=1/2×ON×MN=1/2×2√3×2=2√3 cm²。
11. 如图,在平面直角坐标系 $xOy$ 中,点 $P$ 的坐标为 $(-4,0)$,动圆 $P$ 的半径为 1,若运动后 $\odot P$ 与 $y$ 轴相切,则点 $P$ 运动的距离为______
3或5
.

答案:3或5
解析:
因为圆与y轴相切时,圆心到y轴的距离等于半径。动圆半径为1,所以圆心P到y轴距离为1,即点P的横坐标为1或-1。原P点坐标为(-4,0),当横坐标为1时,运动距离为1 - (-4) = 5;当横坐标为-1时,运动距离为-1 - (-4) = 3。
12. 如图,在扇形 $OAB$ 中,$\angle AOB = 110^{\circ}$,半径 $OA = 18$,将扇形 $OAB$ 沿过点 $B$ 的直线折叠,点 $O$ 恰好落在 $\overset{\frown}{AB}$ 上的点 $D$ 处,折痕交 $OA$ 于点 $C$,则 $\overset{\frown}{AD}$ 的长为______
$5\pi$
.zyjl.cn/pic18/2025-09-08/198e0430978691a27439409e252e8868.jpg?x-oss-process=image/crop,x_1118,y_1203,w_287,h_273">
答案:$5\pi$
解析:
连结$OD$交$BC$于点$E$,由翻折可知$BC$垂直平分$OD$。
因为$OB = OD$,所以$OE=\frac{1}{2}OD=\frac{1}{2}OB$。
在$Rt\triangle BOE$中,$\sin\angle OBC=\frac{OE}{OB}=\frac{1}{2}$,所以$\angle OBC = 30^{\circ}$。
同理$\angle DBC=\angle OBC = 30^{\circ}$,所以$\angle OBD = 60^{\circ}$。
又因为$OB = OD$,所以$\triangle BOD$是等边三角形,则$\angle BOD = 60^{\circ}$。
已知$\angle AOB = 110^{\circ}$,所以$\angle AOD=\angle AOB-\angle BOD = 110^{\circ}-60^{\circ}=50^{\circ}$。
根据弧长公式$l=\frac{n\pi r}{180}$(其中$n$是圆心角度数,$r$是半径),可得$\overset{\frown}{AD}$的长为$\frac{50\pi×18}{180}=5\pi$。
13. (10 分)如图,圆弧形桥拱的跨度 $AB = 12\ m$,拱高 $CD = 4\ m$,求拱桥所在圆的半径.

答案:设拱桥所在圆的圆心为O,半径为R m。连接OA、OD,OD交AB于点D。
因为CD为拱高,所以OD垂直于AB,AD = AB/2 = 6 m。
设OD = x m,则OC = R m,CD = 4 m,所以OD = OC - CD = R - 4,即x = R - 4。
在Rt△AOD中,OA² = AD² + OD²,即R² = 6² + (R - 4)²。
展开得R² = 36 + R² - 8R + 16,化简得8R = 52,解得R = 6.5。
答:拱桥所在圆的半径为6.5 m。