2025年实验班提优训练八年级数学上册苏科版第133页解析答案

25.如图,在数轴上A点表示数a,B点表示数b,C点表示数c,b是最小的正整数,且a,c满足$|a+2|+(c-6)^2= 0$.
(1)$a=$

-2

,$b=$

,$c=$

.
(2)若将数轴折叠,使得点A与点C重合,则点B与数

表示的点重合.
(3)点A,B,C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和点C分别以每秒1个单位长度和2个单位长度的速度向右运动,假设t秒过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,则$AB=$

3t + 3

,$AC=$

4t + 8

,$BC=$

t + 5

.(用含t的代数式表示)
(4)在(3)的条件下,请问：是否存在一个常数m,使得$m\cdot BC-AB$不随运动时间t的改变而改变？若存在,请求出m和这个不变化的数值；若不存在,请说明理由.

存在.理由如下：m·BC - AB = mt + 5m - 3t - 3 = (m - 3)t + 5m - 3，当m = 3时，不变化的数值为12.

答案：
(1) - 2　1　6　[解析]
∵$|a + 2| + (c - 6)^2 = 0$，b是最小的正整数，
∴a = - 2，b = 1，c = 6.
(2)3　[解析]
∵(6 - 2)÷2 = 2，
∴对称点为2，
　
∴点B表示的数为2×2 - 1 = 3.
(3)3t + 3　4t + 8　t + 5　[解析]AB = 1 + t - (-2 - 2t) = 3t + 3，AC = 6 + 2t - (-2 - 2t) = 4t + 8，BC = 6 + 2t - (1 + t) = t + 5.
(4)存在.理由如下：m·BC - AB = mt + 5m - 3t - 3 = (m - 3)t + 5m - 3，
　
∴当m = 3时，不变化的数值为12.

26.中考新考法数形结合思想证明等量关系数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观,从而可以帮助我们快速解题,初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.

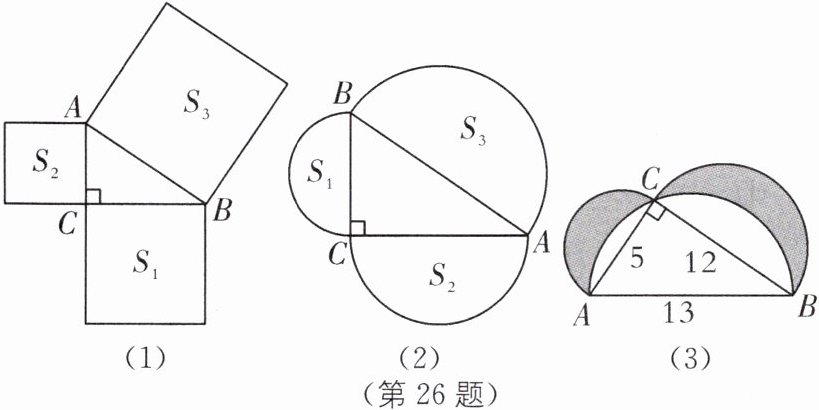
(1)如图(1),在Rt$\triangle ABC$中,$\angle ACB= 90^\circ$,$BC= a$,$AC= b$,$AB= c$,以Rt$\triangle ABC的三边长向外作正方形的面积分别为S_1$,$S_2$,$S_3$,试猜想$S_1$,$S_2$,$S_3$之间存在的等量关系,直接写出结论.
(2)如图(2),如果以Rt$\triangle ABC$的三边长a,b,c为直径向外作半圆,那么第(1)问的结论是否成立？请说明理由.
(3)如图(3),在Rt$\triangle ABC$中,$\angle ACB= 90^\circ$,三边分别为5,12,13,分别以它的三边为直径向上作半圆,求图中阴影部分的面积.

答案：
(1)$S_1 + S_2 = S_3$.
(2)成立.理由如下：
　　设直角三角形两条直角边分别为a，b，斜边为c，
　
∴$S_2 = \frac{1}{2}\pi\cdot(\frac{b}{2})^2 = \frac{b^2\pi}{8}$，$S_1 = \frac{1}{2}\pi\cdot(\frac{a}{2})^2 = \frac{a^2\pi}{8}$，
　$S_3 = \frac{1}{2}\pi\cdot(\frac{c}{2})^2 = \frac{c^2\pi}{8}$.
　
∵$\frac{a^2\pi}{8} + \frac{b^2\pi}{8} = \frac{\pi(a^2 + b^2)}{8} = \frac{\pi c^2}{8} = S_3$，
　
∴$S_1 + S_2 = S_3$.
(3)根据
(2)的结论，两个以直角边为直径的半圆面积等于斜边为直径的半圆面积，故阴影部分的面积 = 两个小半圆的面积
　
∴阴影部分的面积 = $S_{\triangle ABC}$，
　
∴阴影部分的面积为5×12÷2 = 30.