11. 若 $a-b= 2, a-c= \frac{1}{2}$, 则整式 $(c-b)^{2}+3(b-c)+\frac{9}{4}$ 的值为 (
D
)
A.$\frac{9}{2}$
B.$\frac{9}{4}$
C.9
D.0
答案:D 解析:因为$a - b = 2$,$a - c=\frac{1}{2}$,所以$(a - b)-(a - c)=a - b - a + c=-b + c = c - b = 2-\frac{1}{2}=\frac{3}{2}$,所以$b - c=-\frac{3}{2}$,所以原式$=(\frac{3}{2})^{2}+3×(-\frac{3}{2})+\frac{9}{4}=\frac{9}{4}-\frac{9}{2}+\frac{9}{4}=0$。故选D。
12. (1) 若关于 $x, y$ 的两个多项式 $2 m x^{2}-2 x+y$ 与 $-6 x^{2}+2 x-3 y$ 的差中不含二次项, 则 $m=$
-3
.
(2) 已知 $P= 3 a x-8 x+1, Q= x-2 a x-3$, 无论 $x$ 取何值时, $3 P-2 Q= 9$ 恒成立, 则 $a=$
2
.
答案:(1)$-3$;(2)2 解析:因为$P = 3ax - 8x + 1$,$Q = x - 2ax - 3$,无论$x$取何值时,$3P - 2Q = 9$恒成立,所以$3P - 2Q = 3(3ax - 8x + 1)-2(x - 2ax - 3)=9ax - 24x + 3 - 2x + 4ax + 6 = 13ax - 26x + 9=(13a - 26)x + 9 = 9$,所以$13a - 26 = 0$,解得$a = 2$。
解析:
(1)
解:$(2mx^2 - 2x + y) - (-6x^2 + 2x - 3y)$
$=2mx^2 - 2x + y + 6x^2 - 2x + 3y$
$=(2m + 6)x^2 - 4x + 4y$
∵差中不含二次项,
∴$2m + 6 = 0$,解得$m = -3$。
(2)
解:$3P - 2Q = 3(3ax - 8x + 1) - 2(x - 2ax - 3)$
$=9ax - 24x + 3 - 2x + 4ax + 6$
$=(13a - 26)x + 9$
∵无论$x$取何值,$3P - 2Q = 9$恒成立,
∴$13a - 26 = 0$,解得$a = 2$。
答案:(1)$-3$;(2)$2$
13. 新题型 新定义 (2024·北京东城区期末) 对于个位数字不为零的任意三位数 $M$, 将其个位数字与百位数字对调得到 $M^{\prime}$, 则称 $M^{\prime}$ 为 $M$ 的“倒序数”, 将一个数与它的“倒序数”的差的绝对值与 99 的商记为 $F(M)$. 例如 523 为 325 的“倒序数”, $F(325)= \frac{|325-523|}{99}= 2$.
(1) $F(136)=$
5
;
(2) 对于任意三位数 $\overline{a b c}$ 满足: $c>a, F(M)$ 的值是
$c - a$
.
答案:(1)5 解析:由题意可得$F(136)=\frac{|136 - 631|}{99}=5$;(2)$c - a$ 解析:任意三位数$\overline{abc}$,$c > a$,则$F(M)=\frac{|100a + 10b + c-(100c + 10b + a)|}{99}=\frac{99(c - a)}{99}=c - a$。
解析:
(1)解:$F(136)=\frac{|136 - 631|}{99}=\frac{495}{99}=5$
(2)解:设三位数$M=\overline{abc}=100a + 10b + c$,其倒序数$M'=\overline{cba}=100c + 10b + a$。因为$c>a$,所以$F(M)=\frac{|(100a + 10b + c)-(100c + 10b + a)|}{99}=\frac{|99a - 99c|}{99}=\frac{99(c - a)}{99}=c - a$
答案:(1)5;(2)$c - a$
14. 已知 $A= 3 a^{2} b-2 a b^{2}+a b c$, 小明错将“ $2 A-B$ ”看成“ $2 A+B$ ”, 算得结果 $C= 4 a^{2} b-3 a b^{2}+4 a b c$.
(1) 计算 $B$ 的代数式.
(2) 求正确结果的代数式.
(3) 小强说 (2) 中结果的大小与 $c$ 的取值无关, 对吗? 若对, 则当 $a= \frac{1}{8}, b= \frac{1}{5}$ 时, 求 (2) 中代数式的值.
答案:(1)因为$2A + B = C$,所以$B = C - 2A = 4a^{2}b - 3ab^{2}+4abc - 2(3a^{2}b - 2ab^{2}+abc)=4a^{2}b - 3ab^{2}+4abc - 6a^{2}b + 4ab^{2}-2abc=-2a^{2}b + ab^{2}+2abc$;(2)$2A - B = 2(3a^{2}b - 2ab^{2}+abc)-(-2a^{2}b + ab^{2}+2abc)=6a^{2}b - 4ab^{2}+2abc + 2a^{2}b - ab^{2}-2abc = 8a^{2}b - 5ab^{2}$;(3)对,将$a=\frac{1}{8}$,$b=\frac{1}{5}$代入,得$8a^{2}b - 5ab^{2}=8×(\frac{1}{8})^{2}×\frac{1}{5}-5×\frac{1}{8}×(\frac{1}{5})^{2}=0$。
15. (1) 如图①, 两个圆的半径分别为 5 和 3, 两阴影部分的面积分别为 $a, b(a>b)$, 则 $a-b= $
$16\pi$
.
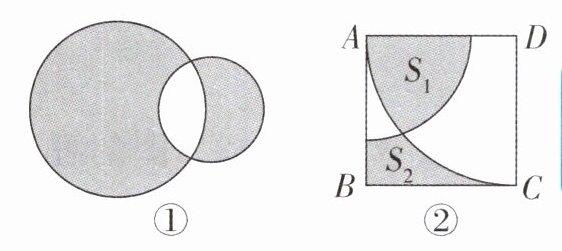
(2) (乐山中考改编) 如图②, $A, B, C, D$ 分别是正方形的四个顶点, 我们将该正方形表示为正方形 $A B C D$, 此时该正方形的边长为 3. 以 $A$ 为圆心, 2 为半径作圆弧, 以 $D$ 为圆心, 3 为半径作圆弧. 若图中阴影部分的面积分别为 $S_{1}, S_{2}$, 则 $S_{1}-S_{2}= $
$\frac{13\pi}{4}-9$
.
答案:(1)$16\pi$ 解析:设重叠部分面积为$c$,所以$a - b=(a + c)-(b + c)=25\pi - 9\pi = 16\pi$;(2)$\frac{13\pi}{4}-9$ 解析:设题图中左侧小空白区域的面积为$m$,由题图可知,$S_{1}+m$是半径为2的四分之一圆的面积,$S_{2}+m$是边长为3的正方形$ABCD$的面积与半径为3的四分之一圆的面积之差,所以$S_{1}-S_{2}=(S_{1}+m)-(S_{2}+m)=\frac{1}{4}×\pi×2^{2}-(3×3-\frac{1}{4}×\pi×3^{2})=\pi-(9-\frac{9\pi}{4})=\frac{13\pi}{4}-9$。
解析:
(1)设重叠部分面积为$c$,则$a - b=(a + c)-(b + c)=\pi×5^{2}-\pi×3^{2}=25\pi - 9\pi = 16\pi$。
(2)设左侧小空白区域的面积为$m$,$S_{1}+m=\frac{1}{4}×\pi×2^{2}$,$S_{2}+m=3×3-\frac{1}{4}×\pi×3^{2}$,$S_{1}-S_{2}=(S_{1}+m)-(S_{2}+m)=\frac{1}{4}×\pi×4-(9-\frac{1}{4}×\pi×9)=\pi - 9+\frac{9\pi}{4}=\frac{13\pi}{4}-9$。
(1)$16\pi$;(2)$\frac{13\pi}{4}-9$
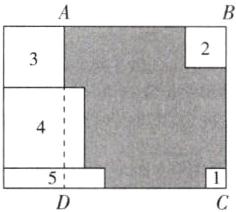
16. 将图①中的长方形纸片剪成 1 号, 2 号, 3 号, 4 号正方形和 5 号长方形.
(1) 设 3 号正方形的边长为 $x, 4$ 号正方形的边长为 $y$, 求 1 号, 2 号正方形的边长分别是多少; (用 $x, y$ 的代数式表示)
(2) 若图①中大长方形纸片的周长为 48, 试求 3 号正方形的边长;
(3) 在 (2) 的情况下, 若将这五个图形按图②的方式放入周长为 100 的长方形中, 求阴影部分的周长.

答案:(1)因为3号正方形的边长为$x$,4号正方形的边长为$y$,所以1号正方形的边长为$y - x$,2号正方形的边长为$x-(y - x)=2x - y$;(2)由(1)得长方形的长为$x + y$,宽为$x+(2x - y)=3x - y$,因为长方形的周长为48,即$2[(x + y)+(3x - y)]=8x = 48$,所以$x = 6$。因为3号正方形的边长为$x$,所以3号正方形的边长为6;(3)如图,由平移知识可知阴影部分的周长为长方形$ABCD$的周长,由(2)可知3号正方形的边长为6,4号正方形的边长为$y$,5号长方形的宽为2号正方形的边长减去1号正方形的边长的差,即$2x - y-(y - x)=3x - 2y = 3×6 - 2y = 18 - 2y$,所以$AD = 6 + y + 18 - 2y = 24 - y$,周长为100的长方形的长为$AB + 6$,宽为$24 - y$,所以$2[AB + 6+(24 - y)]=100$,所以$AB = 20 + y$,则长方形$ABCD$的周长为$[20 + y+(24 - y)]×2 = 88$,即阴影部分的周长为88。