【问题情境】
“数学”的应用包罗万象,在一些看似完全不同的领域中也可能蕴含着“数学”的知识。比如在纺织领域,可以利用数字进行图案设计,不同的数字与不同的排列方式都能组成不同的图景。
【教材呈现】
(1)①已知$\frac {1}{7}= 0.\dot {1}4285\dot {7}$,如图①,将$0.\dot {1}4285\dot {7}$按逆时针方向由内向外螺旋排列填入对应的方格内,请在空白方格内补全对应数字。

②在进行图案设计时,不同的颜色可以表示不同的数字,如图②,该图案是利用某个小数的数字顺序设计的,则这个小数可能是( )
A. $1.\dot {1}4285\dot {7}$
B. $0.0\dot {1}8\dot {5}$
C. $0.\dot {2}1\dot {9}$
D. $π$

【类比探究】
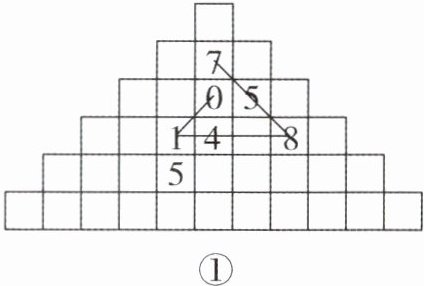
(2)①斐波那契数列是指这样一个数列：$1,1,2,3,5,8,13,21,34… …$这个数列从第3项开始,每一项都等于前两项之和。如图③,共有36个小方格,请设计两种不同的图案,使其填入小方格后分别表示奇数和偶数。之后依照斐波那契数列各项的顺序,自行选择一种排列方式填入图③中。(方格需填满)
②帕多瓦数列与斐波那契数列较为相似,其是指这样一个数列：$1,1,1,2,2,3,4,5,7,9,12… …$这个数列从第4项开始,每一项都等于前面第2项与前面第3项的和,如第5项等于第3项与第2项的和。使用上一小问设计的图案与排列方式,则第4行第3列的小方格中的图案是什么？请说明理由。
【拓展创新】
(3)卢卡斯数列由(2)中的斐波那契数列变形而得,不同的是其第1项和第2项分别是1和3,从第3项开始,每一项都等于前两项之和。通过计算发现,卢卡斯数列各项的末位数字具有规律性。
①卢卡斯数列中第100项的末位数字为____。
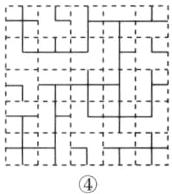
②随机迷宫的构建：如图④,用小方格中的不同图案表示不同的数字,小方格内的实线表示“道路”(不含小方格的边)。卢卡斯数列的每一项可用其末位数字对应的图案代表,请将卢卡斯数列排列在图⑤中构成一个可行的“迷宫”,使该“迷宫”的起点和终点分别位于大正方形的一组对边上,且起点和终点之间有可通行“道路”。