2025年学霸题中题七年级数学上册苏科版第187页解析答案

25. (11分)将一张等边三角形纸片剪成四个大小、形状一样的小等边三角形(如图所示),记为第一次操作,然后将其中右下角的等边三角形又按同样的方法剪成四小片,记为第二次操作,若每次都把右下角的等边三角形按此方法剪成四小片,如此循环进行下去.

(1)如果剪n次共能得到

3n + 1

个等边三角形.
(2)若原等边三角形的边长为1,设$a_{n}$表示第n次所剪出的小等边三角形的边长,如$a_{1}= \frac {1}{2}.$
①试用含n的式子表示$a_{n}= $

$(\frac{1}{2})^{n}$

;
②计算$a_{1}+a_{2}+a_{3}+... +a_{n}= $

$1-\frac{1}{2^{n}}$

.
(3)运用(2)的结论,计算$\frac {1}{3}+\frac {1}{6}+\frac {1}{12}+\frac {1}{24}+\frac {1}{48}+\frac {1}{96}+\frac {1}{192}+\frac {1}{384}+\frac {1}{768}$的值.

$\frac{1}{3}+\frac{1}{6}+\frac{1}{12}+\frac{1}{24}+\frac{1}{48}+\frac{1}{96}+\frac{1}{192}+\frac{1}{384}+\frac{1}{768}=\frac{1}{3}×(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}+\frac{1}{256})=\frac{1}{3}×[1+\frac{1}{2}+(\frac{1}{2})^{2}+(\frac{1}{2})^{3}+(\frac{1}{2})^{4}+(\frac{1}{2})^{5}+(\frac{1}{2})^{6}+(\frac{1}{2})^{7}+(\frac{1}{2})^{8}]=\frac{1}{3}×[1 + 1-(\frac{1}{2})^{8}]=\frac{1}{3}×(1 + 1-\frac{1}{256})=\frac{1}{3}×\frac{511}{256}=\frac{511}{768}$

答案：(1)$(3n + 1)$ (2)①$(\frac{1}{2})^{n}$ ②$1-\frac{1}{2^{n}}$ (3)$\frac{1}{3}+\frac{1}{6}+\frac{1}{12}+\frac{1}{24}+\frac{1}{48}+\frac{1}{96}+\frac{1}{192}+\frac{1}{384}+\frac{1}{768}=\frac{1}{3}×(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}+\frac{1}{256})=\frac{1}{3}×[1+\frac{1}{2}+(\frac{1}{2})^{2}+(\frac{1}{2})^{3}+(\frac{1}{2})^{4}+(\frac{1}{2})^{5}+(\frac{1}{2})^{6}+(\frac{1}{2})^{7}+(\frac{1}{2})^{8}]=\frac{1}{3}×[1 + 1-(\frac{1}{2})^{8}]=\frac{1}{3}×(1 + 1-\frac{1}{256})=\frac{1}{3}×\frac{511}{256}=\frac{511}{768}$

解析：

(1) $3n + 1$
(2) ① $\left(\frac{1}{2}\right)^n$
② $1 - \frac{1}{2^n}$
(3) $\frac{1}{3} + \frac{1}{6} + \frac{1}{12} + \frac{1}{24} + \frac{1}{48} + \frac{1}{96} + \frac{1}{192} + \frac{1}{384} + \frac{1}{768}$
$= \frac{1}{3} × \left(1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{128} + \frac{1}{256}\right)$
$= \frac{1}{3} × \left[1 + \left(\frac{1}{2} + \left(\frac{1}{2}\right)^2 + \left(\frac{1}{2}\right)^3 + \left(\frac{1}{2}\right)^4 + \left(\frac{1}{2}\right)^5 + \left(\frac{1}{2}\right)^6 + \left(\frac{1}{2}\right)^7 + \left(\frac{1}{2}\right)^8\right)\right]$
$= \frac{1}{3} × \left[1 + \left(1 - \left(\frac{1}{2}\right)^8\right)\right]$
$= \frac{1}{3} × \left(2 - \frac{1}{256}\right)$
$= \frac{1}{3} × \frac{511}{256}$
$= \frac{511}{768}$

26. (12分)(2024·宿迁期末)定义:如果$∠α=2∠β+∠γ$,则称$∠α是∠β,∠γ$的加权伴随角.例如:$∠α=50^{\circ },∠β=20^{\circ },∠γ=10^{\circ }$,此时$∠α=2∠β+∠γ$,所以$∠α是∠β,∠γ$的加权伴随角.而$2∠γ+∠β= 40^{\circ }$,所以$∠α不是∠γ,∠β$的加权伴随角.
应用:
(1)如果$∠1= 30^{\circ },∠2= 40^{\circ },∠3= 100^{\circ }.$
①$∠3$____

是

(填“是”或“不是”)$∠1,∠2$的加权伴随角;
②$∠3$____

不是

(填“是”或“不是”)$∠2,∠1$的加权伴随角.
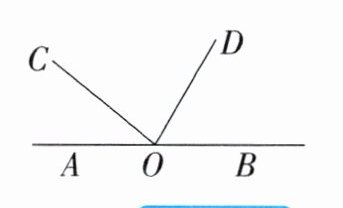
(2)如图,点O在直线AB上,点C,D分别为射线OA,OB上一点,射线OC以每秒$10^{\circ }$顺时针旋转,同时射线OD以每秒$15^{\circ }$逆时针旋转,设旋转的时间为$t(0＜t＜12)s.$
①当$t= 3$时,判断$∠COD是否为∠AOC,∠BOD$的加权伴随角,并说明理由;
②若$∠AOC= 2∠COD$,求t的值;
③在$∠AOC,∠COD,∠BOD$三个角中,若$∠BOD$是另外两个角的加权伴随角,直接写出t的值.

(2)①$∠COD$是$∠AOC,∠BOD$的加权伴随角.理由:当$t = 3$时,$∠AOC = 3×10^{\circ}=30^{\circ},∠BOD = 3×15^{\circ}=45^{\circ},∠COD = 180^{\circ}-30^{\circ}-45^{\circ}=105^{\circ}$，所以$∠COD = 2∠AOC + ∠BOD$，所以$∠COD$是$∠AOC,∠BOD$的加权伴随角 ②$t = 6$或$t = 9$ ③$t=\frac{72}{11}$或$t = 8$

答案：(1)①是 ②不是 (2)①$∠COD$是$∠AOC,∠BOD$的加权伴随角.理由:当$t = 3$时,$∠AOC = 3×10^{\circ}=30^{\circ},∠BOD = 3×15^{\circ}=45^{\circ},∠COD = 180^{\circ}-30^{\circ}-45^{\circ}=105^{\circ}$，所以$∠COD = 2∠AOC + ∠BOD$，所以$∠COD$是$∠AOC,∠BOD$的加权伴随角 ②$t = 6$或$t = 9$ ③$t=\frac{72}{11}$或$t = 8$

解析：

(1)①是
②不是
(2)①$∠COD$是$∠AOC,∠BOD$的加权伴随角.
理由：当$t=3$时，$∠AOC=10^{\circ}×3=30^{\circ}$，$∠BOD=15^{\circ}×3=45^{\circ}$.
$∠COD=180^{\circ}-∠AOC-∠BOD=180^{\circ}-30^{\circ}-45^{\circ}=105^{\circ}$.
$2∠AOC+∠BOD=2×30^{\circ}+45^{\circ}=105^{\circ}$.
$\therefore ∠COD=2∠AOC+∠BOD$，即$∠COD$是$∠AOC,∠BOD$的加权伴随角.
②由题意得$∠AOC=10t^{\circ}$，$∠BOD=15t^{\circ}$，$∠COD=180^{\circ}-10t^{\circ}-15t^{\circ}=180^{\circ}-25t^{\circ}$.
当$∠AOC=2∠COD$时，$10t=2(180-25t)$，解得$t=6$；
当$∠AOC=2∠COD'$（$OC$与$OD$重合后），$∠COD'=25t^{\circ}-180^{\circ}$，$10t=2(25t-180)$，解得$t=9$.
$\therefore t=6$或$t=9$.
③$t=\frac{72}{11}$或$t=8$.