19. (12分)(2025·北京期末)新年前夕,某班计划用一些长方形的卡纸,为同学们制作棱长为10cm的正方体心愿语盒。设计组提供了如图①所示的两种心愿语盒的展开图,制作组按照展开图可围成如图②所示的心愿语盒(不考虑接缝)。
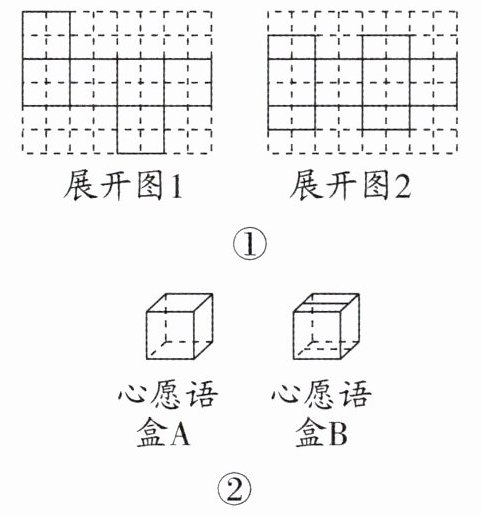
(1)按展开图2可以围成心愿语盒______(填“A”或“B”)。
(2)材料组准备了以下三种类型的卡纸供选择,规格、成本如下表:
|卡纸型号|型号Ⅰ|型号Ⅱ|型号Ⅲ|
|卡纸规格(单位:cm)|30×40|40×60|50×80|
|卡纸成本(单位:元/张)|2|5|8|

①设计组用一张型号Ⅱ的卡纸,最多可以画出______个心愿语盒A的展开图,或______个心愿语盒B的展开图;
②制作组要制作16个心愿语盒。如果你是设计组的成员,请合理选择展开图的样式、卡纸的型号和数量,使所选卡纸的总成本最低,写出你的方案。
我的方案是:型号I的卡纸______张,型号Ⅱ的卡纸______张,型号Ⅲ的卡纸______张,所选卡纸的总成本是______元。
答案:(1)B 解析:心愿语盒B的底面和对应的顶面都是由两个长方形拼合成,所以展开图2可以围成心愿语盒B. (2)①2 3 解析:如图①,一张型号II的卡纸,最多可以画出2个心愿语盒A的展开图;如图②,可以画出3个心愿语盒B的展开图


②1 1 2 23 解析:如图③,型号III卡纸,每张卡纸可制作6个心愿语盒B,则每个心愿语盒B成本为$\frac{8}{6}=\frac{4}{3}$(元),每张卡纸可制作不到6个心愿语盒A,则每个心愿语盒A成本大于$\frac{8}{6}=\frac{4}{3}$(元),

由①得型号II卡纸,每张这样的卡纸可制作2个心愿语盒A或3个心愿语盒B,则每个心愿语盒B成本为$\frac{5}{3}$元,每个心愿语盒A成本为$\frac{5}{2}$元,型号I卡纸,每张这样的卡纸可制作1个心愿语盒A或1个心愿语盒B,则每个心愿语盒B成本为2元,每个心愿语盒A成本为2元,所以可选择型号III卡纸2张,型号II卡纸1张,型号I卡纸1张,则6×2+3+1=16(个),此时总成本最低,所以所用卡纸总费用为8×2+5+2=23(元). 所以我的方案是:型号I的卡纸1张,型号II的卡纸1张,型号III的卡纸2张,所选卡纸的总成本是23元