1. (济宁中考)如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面加了阴影,该几何体的表面展开图是 (
B
)
答案:B 解析:展开图中四个三角形均分离,故加阴影的正方形一定与三角形连接,A、C选项错误,同时底面正方形应不与三角形连接,D选项错误,故选B.
2. (1)如图①,一个正方体纸盒的棱长为 4 cm,将它的一些棱剪开展成一个平面图形,则这个平面图形的周长为______cm.
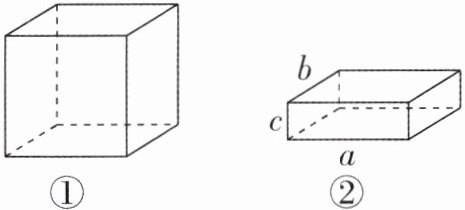
(2)如图②,一个长方体纸盒的长、宽、高分别是 a cm,b cm,c cm(a>b>c),将它的一些棱剪开展成一个平面图形,则这个平面图形的周长的最大值是______cm.
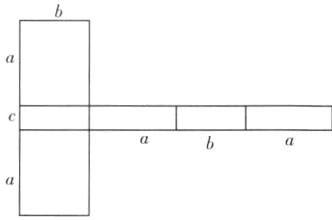
答案:(1)56 解析:因为正方体有6个表面,12条棱,要展成一个平面图形必须要有5条棱连接,所以要剪开12 - 5 = 7(条)棱,则这个平面图形的周长为4×(7×2)=56(cm). (2)(8a + 4b + 2c) 解析:由题意得,需将最长的棱都剪开,最短的棱只剪一条即可得到周长最大的展开图形.如图所示,则这个平面图形的周长的最大值为a×8 + b×4 + c×2 = (8a + 4b + 2c)cm.
3. (2025·邢台模拟)将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,则下列序号中不应剪去的是 (
B
)
A.6
B.3
C.2
D.1
答案:B
解析:
要使余下部分能折成正方体,其展开图需符合“1-4-1”型且无重叠面。原图形中,若剪去3,剩余部分为“1-4-1”标准展开图(1、2、5、6为中间4个,3被剪去后4、7分别为上下各1个),可折成正方体;若剪去1、2、6,会出现田字格或重叠面,无法折成正方体。
不应剪去的是3。
答案:B
4. 现有①②③④四种型号的铁皮,铁皮的形状与相关尺寸如图所示(单位:dm).从中选两种,正好可以制成一个无盖圆柱形水桶(不计接头),则所选的这两种铁皮的型号是 (
C
)
A.①③
B.①④
C.②③
D.②④
答案:C 解析:圆柱侧面展开图的一条边的长等于其底面圆的周长,直径为2 dm的圆的周长为2π dm,直径为4 dm的圆的周长为4π dm,故选择②和③合适.故选C.
5. (2024·扬州期末)小明在学习了《转化 表达》这一课后,掌握了长方体盒子的制作方法.如图是他制作的一个半成品的平面图:
(1)在图中补充一个长方形,使该平面图能折叠成一个长方体盒子;
(2)已知小明制作长方体的盒子长是宽的 2 倍,宽是高的 2 倍,且长方体所有棱长的和为 56 cm,求这个长方体盒子的体积.

答案:(1)答案不唯一,如图所示,补充长方形ABCD.

(2)设长方体的高为a cm,则宽为2a cm,长为4a cm,根据题意得4(a + 2a + 4a)=56,解得a = 2,所以这个长方体的高为2 cm,宽为4 cm,长为8 cm,所以这个长方体盒子的体积为2×4×8 = 64(cm³).
6. (2025·南京期末)观察下图,把右边的图形绕着给定的直线旋转一周后

可能形成的立体图形是 (
D
)

答案:D
解析:
解:右边的图形绕给定直线旋转一周,根据面动成体的原理,形成的立体图形是选项D中的图形。
答案:D
7. 如图是由直角三角形和正方形拼成的四边形.
(1)将这个四边形绕图中虚线旋转一周,可以得到一个立体图形,这能说明的事实是______.(选择正确的一项序号)①点动成线;②线动成面;③面动成体.
(2)求得到的立体图形的体积.$(V_{圆柱}= πr^{2}h,V_{圆锥}= \frac {1}{3}πr^{2}h$,r 为圆柱和圆锥底面半径,h 为圆柱和圆锥的高,结果保留 π)

(1)
③
(2)
因为 $ V_{圆柱}=\pi r^{2}h=\pi×3^{2}×(2 + 3)=45\pi $, $ V_{圆锥}=\frac{1}{3}\pi r^{2}h=\frac{1}{3}×\pi×3^{2}×2 = 6\pi $,所以 $ V = V_{圆柱}-V_{圆锥}=45\pi - 6\pi = 39\pi $.
答案:(1)③ (2)因为 $ V_{圆柱}=\pi r^{2}h=\pi×3^{2}×(2 + 3)=45\pi $, $ V_{圆锥}=\frac{1}{3}\pi r^{2}h=\frac{1}{3}×\pi×3^{2}×2 = 6\pi $,所以 $ V = V_{圆柱}-V_{圆锥}=45\pi - 6\pi = 39\pi $.
解析:
(1)③
(2)解:由题意得,旋转后圆柱的底面半径$r = 3$,高$h=2 + 3=5$,圆锥的底面半径$r = 3$,高$h = 2$。
$V_{圆柱}=\pi r^{2}h=\pi×3^{2}×5 = 45\pi$,
$V_{圆锥}=\frac{1}{3}\pi r^{2}h=\frac{1}{3}×\pi×3^{2}×2=6\pi$,
$V = V_{圆柱}-V_{圆锥}=45\pi-6\pi = 39\pi$。
答:得到的立体图形的体积为$39\pi$。