2025年学霸题中题七年级数学上册苏科版第120页解析答案

15.观察与思考:我们知道1 + 2 + 3 + … + n = $\frac{n(n + 1)}{2}$,那么1^3 + 2^3 + 3^3 + … + n^3结果等于多少呢?请你仔细观察,找出下面图形与算式的关系,解决下列问题:

1^3 = 1^2;1^3 + 2^3 = 3^2;1^3 + 2^3 + 3^3 = 6^2;1^3 + 2^3 + 3^3 + 4^3 = 10^2.
(1)规律观察:1^3 + 2^3 + 3^3 + 4^3 + 5^3 =

^2;
(2)推算概括:用含n的式子表示出1^3 + 2^3 + 3^3 + … + n^3 =

[$\frac{n(n+1)}{2}$]²

;
(3)拓展应用:$\frac{1^3 + 2^3 + 3^3 + … + 100^3}{1 + 2 + 3 + … + 100}$ =

5050

答案：(1)15 解析：因为1³=1²，1³+2³=(1+2)²=3²，1³+2³+3³=(1+2+3)²=6²，1³+2³+3³+4³=(1+2+3+4)²=10²，所以1³+2³+3³+4³+5³=(1+2+3+4+5)²=15²。(2)[$\frac{n(n+1)}{2}$]² 解析：由(1)得1³+2³+3³+…+n³=(1+2+3+…+n)²=[$\frac{n(n+1)}{2}$]²。(3)5050 解析：$\frac{1³+2³+3³+...+100³}{1+2+3+...+100}$=$\frac{(1+2+3+...+100)²}{1+2+3+...+100}$=1+2+3+...+100=$\frac{100×(100+1)}{2}$=5050。

解析：

(1)15
(2)$\left[\frac{n(n+1)}{2}\right]^2$
(3)5050

16.(2025·南京期末)按图示切割正方体就可以切割出正六边形(正六边形的各顶点恰是其棱的中点),以下此正方体的平面展开图及切割线的画法正确的有

①③④

.(填序号)

答案：①③④ 解析：对于①，将展开图重新折叠可得出原来的正方体(含切割线)，符合题意；对于②，将展开图重新折叠不能得出原来的正方体(含切割线)，不符合题意；对于③，将展开图重新折叠可得出原来的正方体(含切割线)，符合题意；对于④，将展开图重新折叠可得出原来的正方体(含切割线)，符合题意。故答案为①③④。

17.新趋势项目式学习 (2025·龙岩期末)【综合与实践】
“好学小组”和“乐学小组”开展了“长方体纸盒的制作”实践活动.他们利用边长为a cm的正方形纸板设计成如图所示的甲、乙两种纸盒,甲种纸盒是无盖的纸盒,乙种纸盒是有盖的纸盒.

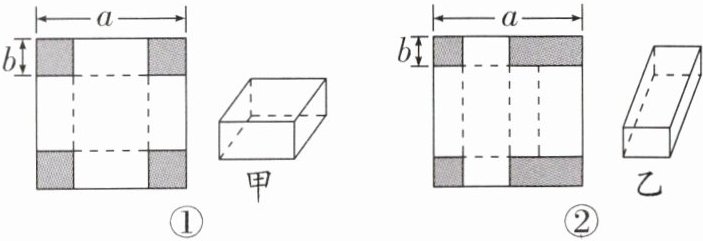
【动手操作】好学小组:根据图①方式制作一个甲种无盖的长方体盒子.方法是先在纸板四角剪去四个同样大小边长为b cm的小正方形,再沿虚线折合起来.乐学小组:根据图②方式制作一个乙种有盖的长方体纸盒.方法是先在纸板四角剪去两个同样大小边长为b cm的小正方形和两个同样大小的小长方形,再沿虚线折合起来.

【问题解决】
(1)①无盖长方体纸盒的底面积为______cm^2(用含a和b的代数式表示);
②有盖长方体纸盒的底面周长为______cm(用含a和b的代数式表示).
【拓展探究】
(2)两小组探究发现:按照上面的制作方案,甲种纸盒的体积和乙种纸盒的体积的比$\frac{V_{甲}}{V_{乙}}$与a,b取值无关.请你写出$\frac{V_{甲}}{V_{乙}}$的值,并说明理由.
【实际应用】
(3)春节临近,杭城某纸箱厂接到一笔订单,需要赶制长、宽、高分别为40cm、30cm、10cm的有盖长方体盒子若干.为了降低成本,提高效率,厂方决定购买大小合适的长方形纸板,采用乙种纸盒的制作方案,并且一张纸板制作一个纸盒.
①请分别在图③、图④虚线框内画出两种不同的设计图,并标上相应的尺寸;
②求厂方采购的长方形纸板的最小面积.

答案：
(1)①(a−2b)²②3(a−2b) 解析：底面长方形的宽为(a−2b)÷2=$\frac{1}{2}$(a−2b)=($\frac{1}{2}$a−b)cm，底面周长为2(a−2b+$\frac{1}{2}$a−b)=2($\frac{3}{2}$a−3b)=3(a−2b)(cm)。(2)V甲:V乙=2:1。理由如下：依题意得V甲=(a−2b)²·b，V乙=(a−2b)·$\frac{1}{2}$(a−2b)·b=$\frac{1}{2}$(a−2b)²·b，所以$\frac{V甲}{V乙}$=$\frac{(a−2b)²·b}{\frac{1}{2}(a−2b)²·b}$=2，所以V甲:V乙=2:1。(3)①两种不同的设计图如下：

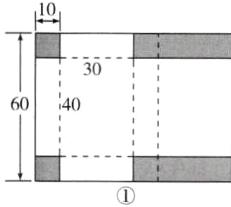
②图①中长方形纸板的面积为S3=60×80=4800(cm²)，图②中长方形纸板的面积为S4=50×100=5000(cm²)，因为4800＜5000，所以厂方采购的长方形纸板的最小面积为4800cm²。