12. 某工艺品车间有20名工人,平均每人每天可制作12个大花瓶或10个小饰品,已知2个大花瓶与5个小饰品配成一套,则要安排
5
名工人制作大花瓶,才能使每天制作的大花瓶和小饰品刚好配套。
答案:5
解析:
解:设安排$x$名工人制作大花瓶,则安排$(20 - x)$名工人制作小饰品。
每天制作大花瓶的数量为$12x$个,每天制作小饰品的数量为$10(20 - x)$个。
因为$2$个大花瓶与$5$个小饰品配成一套,所以配套时大花瓶数量与小饰品数量的比例为$2:5$,可得方程:
$\frac{12x}{10(20 - x)} = \frac{2}{5}$
交叉相乘得:$5×12x = 2×10(20 - x)$
$60x = 20(20 - x)$
$60x = 400 - 20x$
$60x + 20x = 400$
$80x = 400$
$x = 5$
答:要安排$5$名工人制作大花瓶。
13. 如图,将三个相同的小长方形沿“横-竖-横”的顺序排列在一个长为5.7cm,宽为4.5cm的长方形中,则图中空白部分的面积等于
18.06
$cm^{2}$。
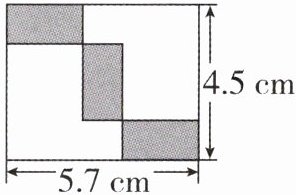
答案:18.06 解析:设小长方形的长为 $ x \, \text{cm} $,则宽为 $ (5.7 - 2x) \, \text{cm} $,由题意得 $ 2(5.7 - 2x) + x = 4.5 $,解得 $ x = 2.3 $,则宽为 $ 5.7 - 2 × 2.3 = 1.1(\text{cm}) $,题图中空白部分的面积为 $ 5.7 × 4.5 - 3 × 2.3 × 1.1 = 18.06(\text{cm}^2) $.
14. 设一列数$a_{1}$,$a_{2}$,$a_{3}$,…,$a_{2023}$,…中任意三个相邻数之和都是35,已知$a_{3}= 2x$,$a_{20}= 15$,$a_{99}= 3 - x$,那么$a_{2026}= $
18
。
答案:18 解析:因为任意三个相邻数之和都是 35,所以 $ a_1 + a_2 + a_3 = a_2 + a_3 + a_4 = 35 $, $ a_2 + a_3 + a_4 = a_3 + a_4 + a_5 = 35 $, $ a_3 + a_4 + a_5 = a_4 + a_5 + a_6 = 35 $,所以 $ a_1 = a_4 $, $ a_2 = a_5 $, $ a_3 = a_6 $,所以 $ a_1 = a_{3n + 1} $, $ a_2 = a_{3n + 2} $, $ a_3 = a_{3n + 3} $.因为 $ 20 = 3 × 6 + 2 $, $ a_{20} = 15 $,所以 $ a_{20} = a_2 = 15 $.因为 $ 99 = 3 × 32 + 3 $,所以 $ a_{99} = a_3 $.因为 $ a_3 = 2x $, $ a_{99} = 3 - x $,所以 $ 3 - x = 2x $,解得 $ x = 1 $.所以 $ a_3 = 2 $.因为 $ a_1 + a_2 + a_3 = 35 $,所以 $ a_1 = 18 $.因为 $ 2026 = 675 × 3 + 1 $,所以 $ a_{2026} = a_1 = 18 $.
解析:
解:因为任意三个相邻数之和都是35,所以$a_{1}+a_{2}+a_{3}=a_{2}+a_{3}+a_{4}=35$,可得$a_{1}=a_{4}$;同理$a_{2}=a_{5}$,$a_{3}=a_{6}$,即该数列是以3为周期循环的周期数列,规律为$a_{1}=a_{3n+1}$,$a_{2}=a_{3n+2}$,$a_{3}=a_{3n+3}$($n$为非负整数)。
因为$20=3×6+2$,所以$a_{20}=a_{2}=15$。
因为$99=3×32+3$,所以$a_{99}=a_{3}$,又$a_{3}=2x$,$a_{99}=3 - x$,则$2x=3 - x$,解得$x=1$,所以$a_{3}=2×1=2$。
由$a_{1}+a_{2}+a_{3}=35$,得$a_{1}=35 - a_{2}-a_{3}=35 - 15 - 2=18$。
因为$2026=3×675+1$,所以$a_{2026}=a_{1}=18$。
18
15. (12分)解下列方程:
(1)$7 - 2x = 3 - 4(x - 2)$;
(2)$\frac{1}{3}(x - 5)= 3-\frac{2(x - 5)}{3}$;
(3)$\frac{0.8 - 9x}{1.2}-\frac{1.3 - 3x}{0.2}= \frac{5x + 1}{0.3}$。
答案:(1) $ x = 2 $ (2) $ x = 8 $ (3) $ x = -1 $
解析:
(1)解:7 - 2x = 3 - 4(x - 2)
7 - 2x = 3 - 4x + 8
-2x + 4x = 3 + 8 - 7
2x = 4
x = 2
(2)解:$\frac{1}{3}(x - 5)= 3-\frac{2(x - 5)}{3}$
x - 5 = 9 - 2(x - 5)
x - 5 = 9 - 2x + 10
x + 2x = 9 + 10 + 5
3x = 24
x = 8
(3)解:$\frac{0.8 - 9x}{1.2}-\frac{1.3 - 3x}{0.2}= \frac{5x + 1}{0.3}$
$\frac{8 - 90x}{12}-\frac{13 - 30x}{2}= \frac{50x + 10}{3}$
8 - 90x - 6(13 - 30x) = 4(50x + 10)
8 - 90x - 78 + 180x = 200x + 40
90x - 70 = 200x + 40
-110x = 110
x = -1
16. (8分)小明在解方程$\frac{2x - 1}{3}= \frac{x + a}{3}-2$时,去分母得到方程$2x - 1 = x + a - 2$,求得方程的解为$x = 2$。你认为$x = 2是方程\frac{2x - 1}{3}= \frac{x + a}{3}-2$的解吗?如果认为是,请说明理由;如果认为不是,请求出该方程的解。
答案:不是,小明去分母时右边的 -2 没有乘 3. 由题意,得 $ x = 2 $ 是方程 $ 2x - 1 = x + a - 2 $ 的解,所以 $ 4 - 1 = 2 + a - 2 $,解得 $ a = 3 $.把 $ a = 3 $ 代入原方程,得 $ \frac{2x - 1}{3} = \frac{x + 3}{3} - 2 $,解得 $ x = -2 $.即原方程的解为 $ x = -2 $.
解析:
不是。
小明去分母时右边的$-2$没有乘$3$。
因为$x = 2$是方程$2x - 1 = x + a - 2$的解,
所以$2×2 - 1 = 2 + a - 2$,
解得$a = 3$。
将$a = 3$代入原方程,得$\frac{2x - 1}{3} = \frac{x + 3}{3} - 2$,
去分母,得$2x - 1 = x + 3 - 6$,
解得$x = -2$。
即原方程的解为$x = -2$。
17. (8分)(2024·北京中考)为防治污染,保护和改善生态环境,自2023年7月1日起,我国全面实施汽车国六排放标准6b阶段(以下简称“标准”)。对某型号汽车,“标准”要求A类物质排放量不超过35mg/km,A,B两类物质排放量之和不超过50mg/km。已知该型号某汽车的A,B两类物质排放量之和原为92mg/km。经过一次技术改进,该汽车的A类物质排放量降低了50%,B类物质排放量降低了75%,A,B两类物质排放量之和为40mg/km,判断这次技术改进后该汽车的A类物质排放量是否符合“标准”,并说明理由。
答案:符合“标准”.理由:设技术改进后该汽车的 A 类物质排放量为 $ x \, \text{mg/km} $,则 B 类物质排放量为 $ (40 - x) \, \text{mg/km} $,由题意得 $ \frac{x}{1 - 50\%} + \frac{40 - x}{1 - 75\%} = 92 $,解得 $ x = 34 $,因为 $ 34 < 35 $,所以这次技术改进后该汽车的 A 类物质排放量符合“标准”.