9. 如图,一个瓶子的容积为 1 L,瓶内装着一些溶液.当瓶子正放时,瓶内溶液的高度为 30 cm,当瓶子倒放时,空余部分的高度为 10 cm.现将瓶内的溶液全部倒入一个圆柱形的杯子里,杯内溶液的高度为 15 cm,则圆柱形杯子的内底面半径约为 (
B
)
A.2.8 cm
B.4.0 cm
C.5.0 cm
D.6.2 cm
答案:B 解析:设溶液的体积为 x L,那么空余部分的体积为 $\frac{1}{3}x$ L,由题意得 $x + \frac{1}{3}x = 1$,解得 $x = 0.75$.设圆柱形杯子的内底面半径约为 a cm,则 $15πa^{2} = 0.75×1000$,解得 $a ≈ 4.0$,所以圆柱形杯子的内底面半径约为 4.0 cm,故选 B.
10. 轮船在顺水中的速度为 28 km/h,在逆水中的速度为 24 km/h,水面上一漂浮物顺水漂流 20 km,则它漂浮了
10
h.
答案:10 解析:设轮船在静水中的速度为 x km/h.由题意得 $2x = 28 + 24$,解得 $x = 26$,即轮船在静水中的速度为 26 km/h,水流速度为 $28 - 26 = 2(km/h)$,所以该漂浮物漂浮时间为 $\frac{20}{2} = 10(h)$.
解析:
解:设轮船在静水中的速度为 $ x $ km/h。
由题意得 $ 2x = 28 + 24 $,解得 $ x = 26 $。
水流速度为 $ 28 - 26 = 2 $ km/h。
漂浮时间为 $ \frac{20}{2} = 10 $ h。
10
11. 一个五位数最高位上的数字是 2,如果把这个数字移到个位数字的右边,那么所得的数比原来的数的 3 倍多 489,求原数.
答案:设原数的后四位是 x,则原数是 $20000 + x$,移后的数是 $10x + 2$.由题意得 $10x + 2 = 3(20000 + x) + 489$,解得 $x = 8641$,故原数为 28 641.
解析:
解:设原数的后四位是 $ x $,则原数是 $ 20000 + x $,移动后所得的数是 $ 10x + 2 $。
由题意得:
$10x + 2 = 3(20000 + x) + 489$
解方程:
$10x + 2 = 60000 + 3x + 489$
$10x - 3x = 60000 + 489 - 2$
$7x = 60487$
$x = 8641$
原数为 $ 20000 + 8641 = 28641 $。
答:原数是 28641。
12. 某商品月末的进货价比月初的进货价降了 8%,而销售价不变,这样,利润率月末比月初高 10%,则月初的利润率是
15%
.
答案:15% 解析:设月初的利润率为 x%,月初的进货价为 M,则 0.92M 是该商品月末的进货价,可得 $M(1 + x\%) = 0.92M[1 + (x + 10)\%]$,约去 M 得 $1 + x\% = 0.92[1 + (x + 10)\%]$,解得 $x = 15$.故月初的利润率为 15%.
解析:
解:设月初的利润率为 $ x\% $,月初的进货价为 $ M $。
则月末的进货价为 $ 0.92M $,销售价不变,可得:
$ M(1 + x\%) = 0.92M[1 + (x + 10)\%] $
两边同时约去 $ M $:
$ 1 + x\% = 0.92[1 + (x + 10)\%] $
解得 $ x = 15 $。
15%
13. 如图,水平桌面上有个内部装水的长方体箱子,箱内有一个与底面垂直的隔板,且隔板左右两侧的水面高度分别为 40 cm、50 cm,现将隔板抽出,若过程中箱内的水量未改变,且不计箱子及隔板厚度,则根据图中的数据,隔板抽出后水面静止时,箱内的水面高度为
44
cm.
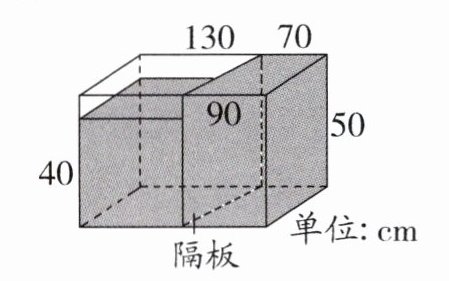
答案:44 解析:设长方体的宽为 x cm,抽出隔板后水面高度为 h cm,长方体的长为 $130 + 70 = 200(cm)$,$200 - 90 = 110(cm)$,根据题意得 $\frac{(130 + 110)x}{2}×40 + \frac{(70 + 90)x}{2}×50 = 200$ $x$ $h$,解得 $h = 44$.所以隔板抽出后水面静止时,箱内的水面高度为 44 cm.
解析:
设长方体的宽为 $ x \, \text{cm} $,抽出隔板后水面高度为 $ h \, \text{cm} $。
长方体的长为 $ 130 + 70 = 200 \, \text{cm} $,隔板左侧底面梯形的下底为 $ 200 - 90 = 110 \, \text{cm} $。
根据水量不变,左侧水的体积为 $ \frac{(130 + 110)x}{2} × 40 $,右侧水的体积为 $ \frac{(70 + 90)x}{2} × 50 $,总体积等于抽出隔板后长方体体积 $ 200 × x × h $。
列方程:
$\frac{(130 + 110)x}{2} × 40 + \frac{(70 + 90)x}{2} × 50 = 200xh$
化简求解:
$\frac{240x}{2} × 40 + \frac{160x}{2} × 50 = 200xh$
$120x × 40 + 80x × 50 = 200xh$
$4800x + 4000x = 200xh$
$8800x = 200xh$
解得 $ h = 44 $。
答:箱内的水面高度为 $ 44 \, \text{cm} $。
14. 七(1)班全体同学进行了一次转盘得分活动.如图,将转盘等分成 8 格,每人转动一次,指针指向的数字就是获得的得分,指针落在边界则重新转动一次.根据小红、小明两位同学的对话,求七(1)班共有学生多少人.

答案:设得 3 分,4 分,5 分和 6 分的共有 x 人,他们平均得分为 y 分.由条件得:(1)得分不足 7 分的人平均得分为 3 分,依题意得 $xy + 3×2 + 5×1 = 3(x + 5 + 3)$,整理得 $xy - 3x = 13$ ①.(2)得 3 分及以上的人平均得分为 4.5 分,依题意得 $xy + 3×7 + 4×8 = 4.5(x + 3 + 4)$,整理得 $4.5x - xy = 21.5$ ②.由①+②得 $xy - 3x + 4.5x - xy = 13 + 21.5$,解得 $x = 23$.故七(1)班共有学生 $23 + 5 + 3 + 4 = 38$(人).
解析:
设得3分、4分、5分和6分的共有$x$人,他们的总得分为$xy$分。
1. 根据得分不足7分的人平均得分为3分:
得分不足7分的人包括得1分(5人)、2分(3人)及3-6分($x$人),总人数为$x + 5 + 3$,总分为$xy + 1×5 + 2×3$。
依题意:$xy + 5 + 6 = 3(x + 8)$,整理得$xy - 3x = 13$ ①。
2. 根据得3分及以上的人平均得分为4.5分:
得3分及以上的人包括3-6分($x$人)、7分(3人)、8分(4人),总人数为$x + 3 + 4$,总分为$xy + 7×3 + 8×4$。
依题意:$xy + 21 + 32 = 4.5(x + 7)$,整理得$4.5x - xy = 21.5$ ②。
3. 联立①②求解:
①+②得:$1.5x = 34.5$,解得$x = 23$。
4. 计算全班总人数:
全班人数为得1分(5人)+得2分(3人)+3-6分(23人)+得7分(3人)+得8分(4人),即$5 + 3 + 23 + 3 + 4 = 38$(人)。
答:七(1)班共有学生38人。