12. 一个三角形的三边长分别为 a,b,c,已知$a:b = 3:2$,$b:c = 4:5$,且该三角形的周长为 30,则$a = $
12
,$b = $
8
,$c = $
10
.
答案:12 8 10 解析:由$a:b=3:2=6:4,b:c=4:5$,得$a:b:c=6:4:5$,故设$a=6n,b=4n,c=5n$.因为该三角形的周长为30,所以$6n+4n+5n=30$,解得$n=2$.故$a=12,b=8,c=10$.
解析:
解:因为$a:b = 3:2 = 6:4$,$b:c = 4:5$,所以$a:b:c = 6:4:5$。
设$a = 6n$,$b = 4n$,$c = 5n$。
由于三角形周长为$30$,则$6n + 4n + 5n = 30$,
$15n = 30$,解得$n = 2$。
所以$a = 6×2 = 12$,$b = 4×2 = 8$,$c = 5×2 = 10$。
$12$;$8$;$10$
13. 用 A,B 两种规格的长方形纸板无重合无缝隙地拼接,可得如图所示的周长为 32 cm 的正方形,已知 A 种长方形的宽为 1 cm,则 B 种长方形的面积是____
12
$cm^{2}$。
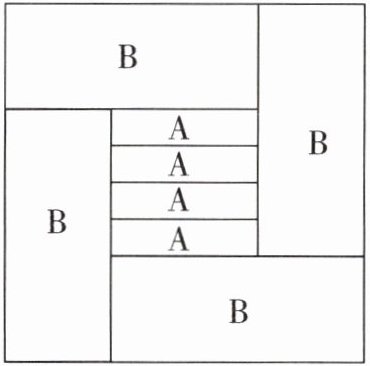
答案:12 解析:设A种长方形的长是x cm,则B种长方形的宽是$(8-x)÷2=(4-\frac{1}{2}x)$cm.由题图可知,B种长方形的长+B种长方形的宽=8 cm,所以B种长方形的长$=8-(4-\frac{1}{2}x)=(4+\frac{1}{2}x)$cm.又B种长方形的长=B种长方形的宽$+4×$A种长方形的宽,所以B种长方形的长$=(4-\frac{1}{2}x)+4=(8-\frac{1}{2}x)$cm,所以$4+\frac{1}{2}x=8-\frac{1}{2}x$,解得$x=4$.所以B种长方形的面积$=(4-\frac{1}{2}x)·(8-\frac{1}{2}x)=(4-2)×(8-2)=2×6=12(cm^{2})$.
解析:
设A种长方形的长是$x$cm。
因为拼接成的正方形周长为32cm,所以正方形边长为$32÷4 = 8$cm。
由题图可知,B种长方形的宽是$(8 - x)÷2=(4-\frac{1}{2}x)$cm。
又因为B种长方形的长+B种长方形的宽=8cm,所以B种长方形的长$=8-(4-\frac{1}{2}x)=(4+\frac{1}{2}x)$cm。
同时,B种长方形的长=B种长方形的宽$+4×$A种长方形的宽(A种宽为1cm),即B种长方形的长$=(4-\frac{1}{2}x)+4=(8-\frac{1}{2}x)$cm。
所以$4+\frac{1}{2}x=8-\frac{1}{2}x$,解得$x = 4$。
则B种长方形的宽为$4-\frac{1}{2}×4=2$cm,长为$8-\frac{1}{2}×4 = 6$cm。
所以B种长方形的面积是$2×6 = 12$cm²。
答案:12
14. 如图,从一张正方形纸片上剪去一个宽为 3 cm 的长方形纸条,再从剩下的长方形纸片上剪去一个宽为 1 cm 的长方形纸条。
(1)如果第一次剪下的长方形纸条的周长恰好是第二次剪下的长方形纸条周长的 2 倍,求原正方形纸片的边长。
(2)第一次剪下的长方形纸条的面积能否是第二次剪下的长方形纸条面积的 2 倍?如果能,请求出正方形纸片的面积;如果不能,请说明理由。

答案:(1)设原正方形纸片的边长为x cm,根据题意得$2(x+3)=2×2(x-3+1)$,解得$x=7$. 答:原正方形纸片的边长为7 cm. (2)不能.理由如下:设原正方形纸片的边长为y cm,假设第一次剪下的长方形纸条的面积是第二次剪下的长方形纸条面积的2倍,则$3y=2×1×(y-3)$,解得$y=-6$,由于y是正整数,所以$y=-6$不符合题意,所以第一次剪下的长方形纸条的面积不可能是第二次剪下的长方形纸条面积的2倍.
15. 阅读理解:a,b,c,d 是有理数,我们把符号$\begin{vmatrix}a&b\\c&d\end{vmatrix} 称为2×2$阶行列式,并且规定:$\begin{vmatrix}a&b\\c&d\end{vmatrix} = ad - bc$,则满足等式$\begin{vmatrix}\frac{x}{2}&\frac{x + 1}{3}\\2&1\end{vmatrix} = 1$的 x 的值是
-10
.
答案:-10 解析:由题意可得$\frac{x}{2}-\frac{2(x+1)}{3}=1$,去分母得$3x-4(x+1)=6$,去括号得$3x-4x-4=6$,移项、合并同类项,得$-x=10$,解得$x=-10$.
解析:
解:由题意可得
$\frac{x}{2} × 1 - 2 × \frac{x + 1}{3} = 1$
即
$\frac{x}{2} - \frac{2(x + 1)}{3} = 1$
去分母,得
$3x - 4(x + 1) = 6$
去括号,得
$3x - 4x - 4 = 6$
移项、合并同类项,得
$-x = 10$
解得
$x = -10$
$-10$
(1)已知关于 x 的一元一次方程$3x + k = 0$是“恰解方程”,则 k 的值为
$\frac{9}{2}$
;
(2)已知关于 x 的一元一次方程$- 2x = mn + n$是“恰解方程”,且解为$x = n(n ≠ 0)$,求$(m + n)(m - n)$的值;
$\frac{77}{9}$
(3)已知关于 x 的一元一次方程$3x = mn + n和- 3x = mn + m$都是“恰解方程”,求代数式$4(mn + n)^{2} - 6(mn + m) - (m - n)$的值。
$\frac{243}{4}$
答案:(1)$\frac{9}{2}$ 解析:$3x+k=0$,解得$x=-\frac{k}{3}$,因为关于x的一元一次方程$3x+k=0$是“恰解方程”,所以$x=3-k$,所以$-\frac{k}{3}=3-k$,解得$k=\frac{9}{2}$. (2)把$x=n$代入关于x的一元一次方程$-2x=mn+n$,所以$-2n=mn+n$,所以$mn=-3n$,所以$m=-3$,且$n≠0$.因为关于x的一元一次方程$-2x=mn+n$是“恰解方程”,即方程为$-2x-mn-n=0$,所以$x=-2-(-mn-n)=-2+mn+n$.因为关于x的一元一次方程$-2x=mn+n$的解为$x=n(n≠0)$,所以$-2+mn+n=n$,所以$mn=2$,所以$-3n=2$,解得$n=-\frac{2}{3}$.因为$m=-3$,所以$(m+n)(m-n)=(-3-\frac{2}{3})×[-3-(-\frac{2}{3})]=-\frac{11}{3}×(-3+\frac{2}{3})=\frac{77}{9}$. (3)解$3x=mn+n$,得$x=\frac{mn+n}{3}$,因为方程$3x=mn+n$是“恰解方程”,所以$x=3+mn+n$,所以$\frac{mn+n}{3}=3+mn+n$,所以$mn+n=-\frac{9}{2}$ ①. 解$-3x=mn+m$,得$x=-\frac{mn+m}{3}$,又因为方程$-3x=mn+m$是“恰解方程”,所以$x=-3+mn+m$,所以$-\frac{mn+m}{3}=-3+mn+m$,所以$mn+m=\frac{9}{4}$ ②, ②-①得$m-n=\frac{27}{4}$,所以$4(mn+n)^{2}-6(mn+m)-(m-n)=4×(-\frac{9}{2})^{2}-6×\frac{9}{4}-\frac{27}{4}=\frac{243}{4}$.
解析:
(1) $\frac{9}{2}$
(2) 解:把$x=n$代入方程$-2x=mn+n$,得$-2n=mn+n$,则$mn=-3n$,因为$n≠0$,所以$m=-3$。
方程$-2x=mn+n$化为$-2x - mn - n = 0$,由“恰解方程”定义得$x=-2 - (-mn - n)=-2 + mn + n$。
又因为方程的解为$x=n$,所以$-2 + mn + n = n$,即$mn=2$。
由$mn=-3n$,得$-3n=2$,解得$n=-\frac{2}{3}$。
则$(m + n)(m - n)=m^2 - n^2=(-3)^2 - \left(-\frac{2}{3}\right)^2=9 - \frac{4}{9}=\frac{77}{9}$。
(3) 解:方程$3x=mn + n$的解为$x=\frac{mn + n}{3}$,由“恰解方程”定义得$x=3 + mn + n$,
所以$\frac{mn + n}{3}=3 + mn + n$,解得$mn + n=-\frac{9}{2}$ ①。
方程$-3x=mn + m$的解为$x=-\frac{mn + m}{3}$,由“恰解方程”定义得$x=-3 + mn + m$,
所以$-\frac{mn + m}{3}=-3 + mn + m$,解得$mn + m=\frac{9}{4}$ ②。
② - ①得$m - n=\frac{9}{4} - \left(-\frac{9}{2}\right)=\frac{27}{4}$。
则$4(mn + n)^2 - 6(mn + m) - (m - n)=4×\left(-\frac{9}{2}\right)^2 - 6×\frac{9}{4} - \frac{27}{4}=4×\frac{81}{4} - \frac{54}{4} - \frac{27}{4}=81 - \frac{81}{4}=\frac{243}{4}$。