1. 把下面的数按要求分一分。
28 30 361 39 402 45 48
50 8 137 74 16 905 1200
(1)奇数:(
361、39、45、137、905
);
偶数:(
28、30、402、48、50、8、74、16、1200
)。
(2)
答案:1.(1)361、39、45、137、905 28、30、402、48、50、8、74、16、1200
(2)
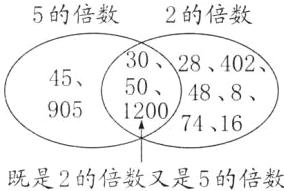
(1)在自然数 1~100 中,奇数有(
50
)个,偶数有(
50
)个;最大的奇数是(
99
),最小的偶数是(
2
);既是 2 的倍数,又是 5 的倍数的最小的数是(
10
),最大的数是(
100
)。
答案:2.(1)50 50 99 2 10 100
(2)47 后面三个连续奇数是(
49、51、53
),前面三个连续偶数是(
42、44、46
)。
答案:2.(2)49、51、53 42、44、46
(3)按要求填数。
① 要使 17□是 2 的倍数,则□里可以填(
0、2、4、6、8
)。
② 要使 2□5 是 5 的倍数,则□里可以填(
0~9
)。
③ 要使 93□既是 2 的倍数,又是 5 的倍数,则□里可以填(
0
)。
答案:2.(3)①0、2、4、6、8 ②0~9 ③0
3. 从 0、1、2、5 中,每次选两个数字,按要求组成一个两位数。(写出所有可能的情况)
(1)组成的数是偶数:(
10、20、50、12、52
)。
(2)组成的数是奇数:(
21、51、15、25
)。
(3)组成的数是 5 的倍数:(
10、20、50、15、25
)。
(4)组成的数既是 2 的倍数,又是 5 的倍数:(
10、20、50
)。
答案:3.(1)10、20、50、12、52 (2)21、51、15、25
(3)10、20、50、15、25 (4)10、20、50
(1)473 至少加上(
A
)是 2 的倍数,至少减去(
A
)是 5 的倍数。
A.1
B.2
C.3
D.4
答案:4.(1)A
(2)(思维过程)一个数加上 2 就是 5 的倍数,这个数的个位一定是(
D
)。
A.0
B.3
C.8
D.3 或 8
答案:4.(2)D
(3)下面的说法中,正确的有(
D
)个。
① 如果 a 是偶数,那么 a+1 一定是奇数。
② 用 2、4、6、8 组成的四位数一定是 2 的倍数。
③ 5 个连续自然数的和不一定是 2 的倍数,但一定是 5 的倍数。
A.0
B.1
C.2
D.3
答案:4.(3)D
解析:
① 偶数加1为奇数,正确。
② 个位为2、4、6、8的数是2的倍数,正确。
③ 设5个连续自然数为$n$,$n+1$,$n+2$,$n+3$,$n+4$,和为$5n+10=5(n+2)$,一定是5的倍数;当$n$为偶数时和为奇数,当$n$为奇数时和为偶数,不一定是2的倍数,正确。
正确的有3个。
D
5.(说理表达)冬冬是个“小问号”,你能回答冬冬的问题吗?

答案:5.因为2×5=10,一个整十数肯定是2和5的倍数,所以判断一个数是不是2和5的倍数只要看个位
6.(探索规律)小明正在弹琴,灯突然不亮了,他去按了开关 5 次,灯依然不亮,妈妈又去按了 5 次,灯还是不亮,原来是停电了,后来他们陆续又按了 21 次。如果来电了,那么灯是不亮的还是亮的?
答案:6.5+5+21=31(次) 不亮 解析:开始是亮的,如果不停电,那么按1次开关,灯是不亮的,按2次开关,灯是亮的,按3次开关,灯是不亮的,按4次开关,灯是亮的……按奇数次开关,灯是不亮的,按偶数次开关,灯是亮的。
解析:
5+5+21=31(次)
按奇数次开关,灯是不亮的,31是奇数,所以灯是不亮的。
不亮