1. 汽油的密度是$0.71×10^{3}kg/m^{3}$,它的物理意义是(
B
)
A.$1kg$汽油的体积是$0.71×10^{3}m^{3}$
B.$1m^{3}$汽油的质量为$0.71×10^{3}kg$
C.$1kg$汽油的密度是$0.71×10^{3}kg/m^{3}$
D.$0.71m^{3}$汽油的质量为$1×10^{3}kg$
答案:1.B
2. (2024·绥化)将一瓶酸奶喝掉一半后,下列关于剩下半瓶酸奶的说法中,正确的是(
D
)
A.质量和密度都不变
B.质量和密度都变为原来的一半
C.质量不变,密度变为原来的一半
D.质量变为原来的一半,密度不变
答案:2.D
3. (2025·徐州新沂期中)人们常说“铁比棉花重”,这实际上是指(
C
)
A.棉花的质量比铁小
B.棉花的体积比铁小
C.棉花的密度比铁小
D.棉花的弹性比铁小
答案:3.C
4. (易错题)两个完全相同的烧杯中装有不同的液体,把它们放在已经平衡的天平上。调节游码的位置后,使天平再次平衡(如图所示),则(
C
)
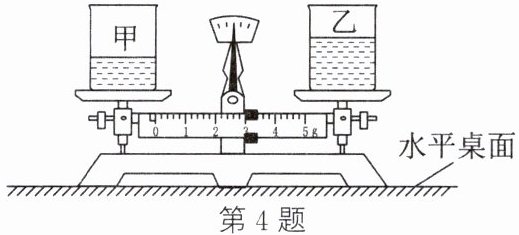
A.甲液体质量较小
B.两种液体质量相等
C.甲液体密度较大
D.两种液体密度相等
答案:4.C [易错分析] 不少同学一看天平横梁平衡,误认为甲、乙两种液体的质量相等,原因是忽视了游码的位置不在零刻度线处。
5. 在密度单位中,$1g/cm^{3}=$_________$kg/m^{3}$。测得一个苹果的质量为$171g$,体积为$180cm^{3}$,则该苹果的密度为
$0.95×10^{3}$
$kg/m^{3}$。
答案:$5.1×10^{3} 0.95×10^{3}$
6. 若用铜做成的铜汤匙和铜锅的质量之比为$1:40$,则它们的体积之比为
1:40
,密度之比为
1:1
。
答案:6.1:40 1:1
7. (2024·无锡新吴期中)在空间站失重环境下,书写并非易事:用钢笔书写,墨水不会自动往下流,导致书写断断续续。因此设计出如图所示的“太空圆珠笔”。书写过程中,笔芯内氮气的质量
不变
,密度
变小
。(变大/不变/变小)
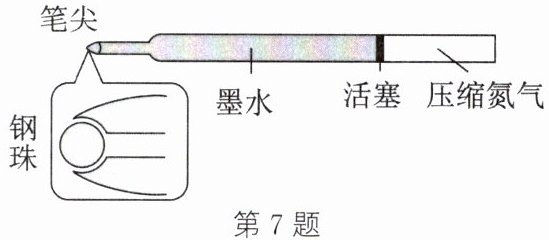
答案:7.不变 变小
8. (2025·南京玄武校级期中)甲、乙两种物体质量之比为$2:1$,体积之比是$4:1$,则甲、乙的密度之比为
1:2
;将甲物体切除$\frac{1}{2}$,乙物体切除$\frac{1}{3}$,甲、乙物体余下的部分,其质量之比为
3:2
,密度之比为
1:2
。
答案:8.1:2 3:2 1:2
9. 金属锇的密度为$22.5×10^{3}kg/m^{3}$,$1m^{3}$白矮星物质的质量是$10^{5}~10^{8}t$,$1cm^{3}$中子星物质的质量是$10^{7}~10^{9}t$,而超巨星物质的密度只有水的密度的千分之一。上述物质中,密度最大的是(
B
)
A.超巨星物质
B.中子星物质
C.白矮星物质
D.金属锇
答案:9.B
解析:
金属锇的密度:$22.5×10^{3}\ \mathrm{kg/m}^3=22.5\ \mathrm{g/cm}^3$;
白矮星物质的密度:$\rho_1=\frac{10^{5}×10^{3}\ \mathrm{kg}}{1\ \mathrm{m}^3}=10^{8}\ \mathrm{kg/m}^3=10^{5}\ \mathrm{g/cm}^3$,$\rho_2=\frac{10^{8}×10^{3}\ \mathrm{kg}}{1\ \mathrm{m}^3}=10^{11}\ \mathrm{kg/m}^3=10^{8}\ \mathrm{g/cm}^3$,即$10^{5}~10^{8}\ \mathrm{g/cm}^3$;
中子星物质的密度:$\rho_3=\frac{10^{7}×10^{6}\ \mathrm{g}}{1\ \mathrm{cm}^3}=10^{13}\ \mathrm{g/cm}^3$,$\rho_4=\frac{10^{9}×10^{6}\ \mathrm{g}}{1\ \mathrm{cm}^3}=10^{15}\ \mathrm{g/cm}^3$,即$10^{13}~10^{15}\ \mathrm{g/cm}^3$;
超巨星物质的密度:$\frac{1}{1000}×1\ \mathrm{g/cm}^3=10^{-3}\ \mathrm{g/cm}^3$。
比较可知,密度最大的是中子星物质,答案选B。
10. (2024·扬州江都段考)如图所示,$A$、$B$、$C$三个完全相同的杯子内,盛有不同体积的水,现将三个质量相同、材料不同的实心金属球甲、乙、丙分别浸没在$A$、$B$、$C$三个杯子的水中(水均未溢出),且杯中水面升高后,恰好相平,则比较甲、乙、丙三个金属球的密度是(
B
)
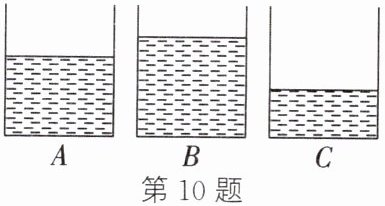
A.甲最大
B.乙最大
C.丙最大
D.一样大
答案:10.B
解析:
解:设杯子底面积为$S$,初始水体积$V_{A水}$、$V_{B水}$、$V_{C水}$,金属球体积$V_{甲}$、$V_{乙}$、$V_{丙}$。
由图知初始水面高度$h_{B水}>h_{A水}>h_{C水}$,则$V_{B水}=Sh_{B水}>V_{A水}=Sh_{A水}>V_{C水}=Sh_{C水}$。
放入球后水面相平,即$h_{A水}+\frac{V_{甲}}{S}=h_{B水}+\frac{V_{乙}}{S}=h_{C水}+\frac{V_{丙}}{S}$,故$V_{甲}=S(h-h_{A水})$,$V_{乙}=S(h-h_{B水})$,$V_{丙}=S(h-h_{C水})$。
因为$h_{B水}>h_{A水}>h_{C水}$,所以$h-h_{B水}<h-h_{A水}<h-h_{C水}$,即$V_{乙}<V_{甲}<V_{丙}$。
已知金属球质量$m$相同,由$\rho=\frac{m}{V}$得$\rho_{乙}>\rho_{甲}>\rho_{丙}$。
结论:乙最大,选B。