一、选择题(每小题 2 分,共 12 分)
1. (2025·泰兴二模)下列多项式中,能用平方差公式进行因式分解的是(
C
)
A.$-a^{2}-b^{2}$
B.$a^{2}+b^{2}$
C.$a^{2}-b^{2}$
D.$a^{2}-b^{2}-1$
答案:1. C
2. (2024·仪征一模)对任意整数$n$,$(2n + 1)^{2}-25$都能(
B
)
A.被 3 整除
B.被 4 整除
C.被 5 整除
D.被 6 整除
答案:2. B
解析:
$(2n + 1)^{2}-25$
$=(2n + 1)^{2}-5^{2}$
$=(2n + 1 + 5)(2n + 1 - 5)$
$=(2n + 6)(2n - 4)$
$=2(n + 3) · 2(n - 2)$
$=4(n + 3)(n - 2)$
因为$n$为整数,所以$(n + 3)(n - 2)$为整数,故$4(n + 3)(n - 2)$能被$4$整除。
B
3. (2025·赣榆区期中)若$49^{8}-14^{2}×7^{12}$的运算结果为$S$,则$S$不能被下列哪个数整除(
D
)
A.5
B.7
C.9
D.11
答案:3. D
解析:
$49^{8}-14^{2}×7^{12}$
$=(7^{2})^{8}-(2×7)^{2}×7^{12}$
$=7^{16}-2^{2}×7^{2}×7^{12}$
$=7^{16}-4×7^{14}$
$=7^{14}(7^{2}-4)$
$=7^{14}×45$
$=7^{14}×5×9$
$S=7^{14}×5×9$,能被5、7、9整除,不能被11整除。
D
4. (2025·沛县期中)如果$x^{2}+mx + 8=(x - 4)(x - 2)$,那么$m$的值为(
D
)
A.6
B.8
C.$-8$
D.$-6$
答案:4. D
解析:
$(x - 4)(x - 2)=x^{2}-2x-4x + 8=x^{2}-6x + 8$,
因为$x^{2}+mx + 8=(x - 4)(x - 2)$,
所以$x^{2}+mx + 8=x^{2}-6x + 8$,
则$m=-6$。
D
5. (2025·江宁区校级一模)若一个正整数能表示为两个连续偶数的平方差,则称这个正整数为“神秘数”(如$4 = 2^{2}-0^{2}$,$12 = 4^{2}-2^{2}$)。在$1∼100$这 100 个数中,“神秘数”的个数是(
D
)
A.10
B.11
C.12
D.13
答案:5. D
解析:
设两个连续偶数为$2k$和$2k+2$($k$为非负整数),则“神秘数”可表示为:
$(2k+2)^2 - (2k)^2 = (4k^2 + 8k + 4) - 4k^2 = 8k + 4 = 4(2k + 1)$
即“神秘数”是$4$的奇数倍。
在$1∼100$中,$4$的倍数有$4,8,12,···,100$,共$25$个。其中奇数倍为$4×1,4×3,4×5,···,4× m$,且$4m ≤ 100$,即$m ≤ 25$。$m$为奇数,取值为$1,3,5,···,25$,共$13$个。
D
6. (2025·姜堰区校级月考)下面有三个结论:①两个连续偶数的平方差一定是 8 的倍数;②两个连续奇数的平方差一定是 8 的倍数;③任意一个个位数是 5 的整数平方后一定是 25 的倍数。其中正确的是(
C
)
A.①②
B.①③
C.②③
D.①②③
答案:6. C
解析:
②设两个连续奇数为$2n-1$,$2n+1$($n$为整数),则$(2n+1)^2-(2n-1)^2=(4n^2 + 4n + 1)-(4n^2 - 4n + 1)=8n$,是8的倍数。
③设个位数是5的整数为$10n+5$($n$为整数),则$(10n+5)^2=100n^2 + 100n + 25=25(4n^2 + 4n + 1)$,是25的倍数。
①设两个连续偶数为$2n$,$2n+2$($n$为整数),则$(2n+2)^2-(2n)^2=(4n^2 + 8n + 4)-4n^2=8n + 4=4(2n + 1)$,是4的倍数,不一定是8的倍数。
正确的是②③。
C
二、填空题(每小题 2 分,共 20 分)
7. (2025·姑苏区校级一模)因式分解:$4x^{2}-4 =$
$ 4(x + 1)(x - 1) $
。
答案:7. $ 4(x + 1)(x - 1) $
8. (2025·锡山区校级四模)因式分解:$2m^{2}-4m + 2 =$
$ 2(m - 1)^2 $
。
答案:8. $ 2(m - 1)^2 $
9. (2025·海门市校级模拟)因式分解:$x^{2}-x - 6 =$
$ (x + 2)(x - 3) $
。
答案:9. $ (x + 2)(x - 3) $
10. (2025·睢宁县期中)已知$m + 2n - 3 = 0$,且$m - 2n + 2 = 0$,则$m^{2}-4n^{2} =$
$ -6 $
。
答案:10. $ -6 $
解析:
由题意得:
$\begin{cases}m + 2n = 3 \\m - 2n = -2\end{cases}$
$m^2 - 4n^2 = (m + 2n)(m - 2n) = 3 × (-2) = -6$
$-6$
11. (2025·邗江区校级期中)若$a + b = 2$,则$a^{2}+b^{2}+2ab =$
4
。
答案:11. 4
解析:
因为$a + b = 2$,根据完全平方公式$(a + b)^2 = a^2 + 2ab + b^2$,所以$a^2 + b^2 + 2ab=(a + b)^2=2^2 = 4$。
4
12. (2025·仪征三模)已知代数式$x - 2y$的值为 3,则代数式$x^{2}-4y^{2}-12y$的值为
9
。
答案:12. 9
解析:
因为$x - 2y = 3$,所以$x = 2y + 3$。
将$x = 2y + 3$代入$x^2 - 4y^2 - 12y$得:
$\begin{aligned}&(2y + 3)^2 - 4y^2 - 12y\\=&4y^2 + 12y + 9 - 4y^2 - 12y\\=&(4y^2 - 4y^2) + (12y - 12y) + 9\\=&0 + 0 + 9\\=&9\end{aligned}$
9
13. 若$x^{2}+6x + k$能分解成一个含$x$的一次多项式的平方,则$k$的值是
9
。
答案:13. 9
解析:
因为$x^{2}+6x + k$能分解成一个含$x$的一次多项式的平方,所以可设$x^{2}+6x + k=(x + a)^{2}$,展开得$x^{2}+2ax + a^{2}$。对比系数可得$2a = 6$,解得$a = 3$,则$k = a^{2}=3^{2}=9$。
9
14. 若关于$x$的二次三项式$x^{2}+2(m - 3)x + 16$可用完全平方公式分解因式,则$m$的值为
7 或 $ -1 $
。
答案:14. 7 或 $ -1 $
解析:
解:因为二次三项式$x^{2}+2(m - 3)x + 16$可用完全平方公式分解因式,所以该二次三项式是一个完全平方式。
完全平方式的形式为$(x\pm a)^{2}=x^{2}\pm 2ax + a^{2}$,对比可得$16 = a^{2}$,则$a = \pm 4$。
当$a = 4$时,$2(m - 3)=2×4$,即$2(m - 3)=8$,解得$m - 3 = 4$,$m = 7$;
当$a = -4$时,$2(m - 3)=2×(-4)$,即$2(m - 3)= - 8$,解得$m - 3 = - 4$,$m = - 1$。
综上,$m$的值为$7$或$-1$。
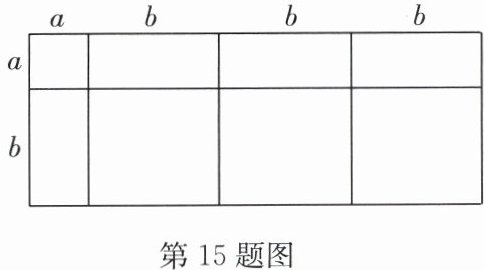
15. (2024·海陵区一模)整式的学习中我们常常使用拼图的方法得出相应的等式,利用如图所示的拼图分解因式:$a^{2}+4ab + 3b^{2} =$
$ (a + 3b)(a + b) $
。
答案:15. $ (a + 3b)(a + b) $