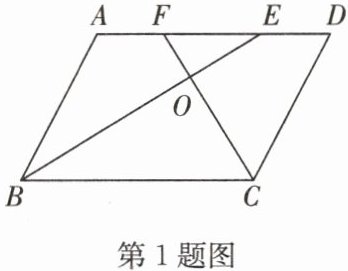
1. 如图,在$□ ABCD$中,$BE$,$CF$分别是$∠ ABC$和$∠ BCD$的平分线,$BE$,$CF$相交于点$O$.
(1) 判断$△ EOF$的形状并说明理由;
(2) 试判断$AF$与$DE$有何数量关系,并说明理由.
答案:1.解:(1)△EOF是直角三角形,理由如下:
∵四边形ABCD是平行四边形,
∴AB//CD,
∴∠ABC+∠BCD=180°.
又
∵BE,CF分别是∠ABC和∠BCD的平分线,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠BCD)=90°,
∴∠BOC=90°=∠EOF,
∴△EOF是直角三角形.
(2)AF=DE,理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,AD//BC,
∴∠AEB=∠EBC;
又
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE.
同理可得CD=DF;
又
∵AB=CD,
∴AE=DF,
∴AF=DE.
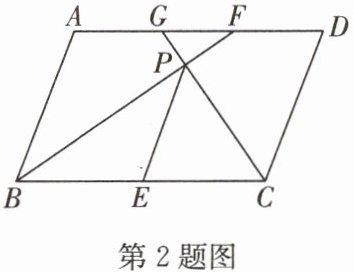
2. 如图,在平行四边形$ABCD$中,$∠ ABC$的平分线$BF$交$AD$于点$F$,$∠ BCD$的平分线$CG$交$AD$于点$G$,两条角平分线在平行四边形内部交于点$P$,点$E$在$BC$上,连接$PE$,$PE = BE$.
(1) 求证:$E$是$BC$的中点;
(2) 若$AB = 4$,$PE = 3$,求$GF$的长.
答案:2.(1)证明:如答图

∵四边形ABCD是平行四边形,
∴AB//CD,AD=BC,
∴∠ABC+∠BCD=180°.
∵BF,CG分别平分∠ABC和∠BCD,
∴∠1=$\frac{1}{2}$∠ABC,∠4=$\frac{1}{2}$∠BCD,
∴∠1+∠4=$\frac{1}{2}$(∠ABC+∠BCD)=$\frac{1}{2}$×180°=90°,
∴∠2+∠3=90°.
∵PE=BE,
∴∠1=∠2,
∴∠3=∠4,
∴PE=CE,
∴BE=CE,
即E是BC的中点.
(2)解:
∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠1=∠AFB;
∵BF平分∠ABC,
∴∠ABF=∠1,
∴∠ABF=∠AFB,
∴AB=AF,
又AB=4,
∴AF=4.
同理DG=CD=AB=4.
∵PE=3,BE=PE=CE,
∴BE=CE=3,
∴AD=BC=BE+CE=6,
∴GF=AF+DG−AD=4+4−6=2.