活动一:直接应用
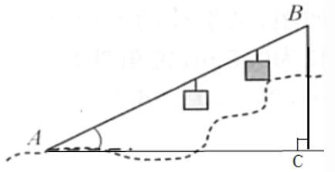
如图 7-12,登山缆车的车厢从点 A 到达点 B 时,缆车行驶了 200 m,在这段路程中缆车行驶的路线与水平面的夹角为 30°.你知道缆车垂直上升的距离是多少吗?

答案:解:过点B作与过点A的水平线的垂线,垂足为C
∵$\angle BAC=3{0}°,$$AB=200\ \mathrm {m}$
∴$BC=\frac {1} {2}\ \mathrm {AB}=100 ({m} )$
答:缆车垂直上升的距离是$100\ \mathrm {m}。$
活动二:间接应用
认真研读课本中的问题 2.
(1) 本题求解的是
点C到地面的高度
;它在图 7-13 中即是
AD
的长度.所求线段长度和已知条件是如何联系的?

(2) 解决下列问题:
① 经过多长时间后,小明离地面的高度最高?
② 从最底部开始,经过多长时间后,小明离地面的高度达到 10.3 m?
③ 在旋转 1 周的过程中,小明有多长时间连续保持离地面 10.3 m 以上?
答案:点C到地面的高度
AD
解:(2)①旋转半周到达最高点,即经过$6\mathrm {\ \mathrm {min}}$
②∵AD= 10.3m
∴BD= 10m
∴OD=OB-BD=10m
$sin∠OCD=\frac {OD}{OC}=\frac {1}{2}$
∴∠OCD=30°
∴∠DOC= 60°
∴摩天轮旋转了$\frac {1}{6}$周或者$\frac {5}{6}$周
∴经过$2\mathrm {\ \mathrm {min}}$或者$10\mathrm {\ \mathrm {min}},$小明离地面的高度达到10.3m
$③10-2=8(\mathrm {\ \mathrm {min}})$
∴小明有8分钟连续保持离地面10.3m 以上
解:通过摩天轮旋转一周的时间以及小明到达点C经过的时间,可以
求出∠DOC的大小。已知圆的半径,可以通过解直角三角形DOC
求出DO的长度,从而求出BD的长度。已知摩天轮底部与地面的距离,
求出AD的长度。
1. 如图所示的衣架可以近似看成一个等腰三角形 $ABC$,其中 $AB = AC$,$\angle ABC = 27°$,$BC = 44 cm$,则高 $AD$ 约为(
B
).

(参考数据:$\sin 27° \approx 0.45$,$\cos 27° \approx 0.89$,$\tan 27° \approx 0.51$)
A.$9.90 cm$
B.$11.22 cm$
C.$19.58 cm$
D.$22.44 cm$
答案:B