4. 在$ Rt\triangle ABC$中,$\angle C = 90°$,$\sin A = \frac{5}{13}$,则$\cos A =$
$\frac{12}{13}$
,$\cos B =$
$\frac{5}{13}$
,$\tan A =$
$\frac{5}{12}$
.
答案:$\frac {12}{13}$
$\frac {5}{13}$
$\frac {5}{12}$
5. 在$ Rt\triangle ABC$中,两边的长分别为$3$和$4$,求此三角形中最小角的正弦值.
答案:解:∵在ABC中,∠B=90°
①当AC=4,BC=3时,$AB=\sqrt{AC²-BC²}=\sqrt{7}$
$sin C =\frac {AB}{AC}=\frac {\sqrt{7}}{4}$
②当AB=3,BC=4时,$AC=\sqrt{AB²+BC²}=5$
$sin C=\frac {AB}{AC}=\frac {3}{5}$
综上,最小角的正弦值为$\frac {\sqrt 7}4$或$\frac 35$
1. 如图,在方格纸中,$A$、$B$、$C$、$D$都是格点,$AB$与$CD$相交于点$P$,则$\cos\angle APC$的值为(
B
).

A.$\frac{\sqrt{3}}{5}$
B.$\frac{2\sqrt{5}}{5}$
C.$\frac{2}{5}$
D.$\frac{\sqrt{5}}{5}$
答案:B
2. 如图,两条宽度都是$1$的纸条交叉叠在一起,且它们的夹角为$\alpha$,则它们重叠部分(图中阴影部分)的面积是(
A
).

A.$\frac{1}{\sin\alpha}$
B.$\frac{1}{\cos\alpha}$
C.$\sin\alpha$
D.$1$
答案:A
3. 如图是引拉线固定电线杆的示意图,已知$CD\perp AB$,$CD = 3\sqrt{3}\ m$,$\angle CAD = \angle CBD = 60°$,则拉线$AC$的长是
6
$m$.

答案:6
4. 观察下列等式:
①$\sin 30° = \frac{1}{2}$,$\sin 60° = \frac{\sqrt{3}}{2}$;②$\sin 45° = \frac{\sqrt{2}}{2}$,$\cos 45° = \frac{\sqrt{2}}{2}$;③$\cos 30° = \frac{\sqrt{3}}{2}$,$\cos 60° = \frac{1}{2}$.
(1) 根据上述规律,计算:$\sin^2\alpha + \sin^2(90° - \alpha) =$
1
[注:$\sin^2\alpha$即$(\sin\alpha)^2$].
(2) 计算:$\sin^2 1° + \sin^2 2° + \sin^2 3° + ·s + \sin^2 89°$.
答案:1
解:原式=sin²1°+sin²89°+sin²2°+sin²88°+...+sin²44°+sin²46°+sin²45°
$ =1+1+1+...+1+\frac{1}{2}$
$ =44\frac{1}{2}$
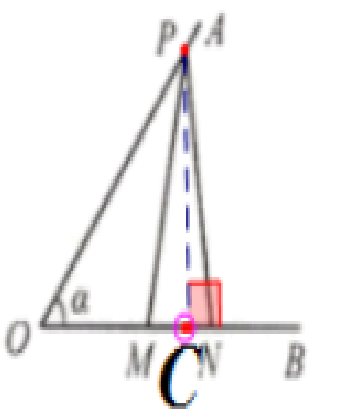
5. 如图,$\angle AOB = \alpha$,点$P$在边$OA$上,$OP = 10$,点$M$、$N$在边$OB$上,$PM = PN$. 若$\sin\alpha = \frac{4}{5}$,$MN = 2$,求$OM$的长和$\tan\angle PMN$的值.

答案:解:过点P 作PC⊥OB交OB于点C
∵$sin α=\frac {PC}{OP}=\frac {4}{5}$
∴PC=8,$OC=\sqrt{OP²-PC²}= 6$
∵PM=PN,PC⊥OB,MN=2
∴MC= NC=1
∴OM=OC-MC= 5
$tan∠PMN=\frac {PC}{MC}=8$