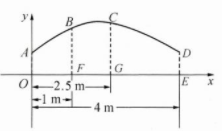
1. 某抛物线形涵洞的截面如图所示. 现测得水面宽 AB = 4 m,涵洞顶点 O 到水面的距离为 1 m,在如图的平面直角坐标系中,点 A 的坐标是
$(2,-1)$
,点 B 的坐标是
$(-2,-1)$
;若把涵洞的截面看作一个二次函数的图像,则相应的函数表达式为
$y = -\frac{1}{4}x^{2}$
.

答案:(2,-1)
(-2,-1)
$y=-\frac 14x^2$
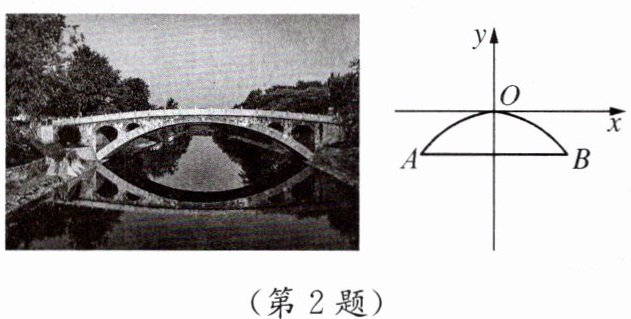
2. 河北省赵县的赵州桥的桥拱可近似看作抛物线形,建立如图所示的平面直角坐标系,其相应的函数表达式为$y = -\frac{1}{25}x^{2}$. 当水位线在 AB 位置时,水面宽 AB = 30 m,这时水面离桥顶的高度 h 是(
D
).
A.5 m
B.6 m
C.8 m
D.9 m
答案:D
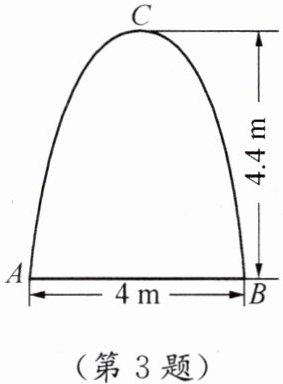
3. 如图,某工厂大门是一抛物线形拱门,现有一辆满载货物的汽车要通过大门,货物顶部距地面 2.8 m,货物宽度为 2.4 m. 请判断这辆汽车能否顺利通过该大门.
答案:3. 以顶点$C$为原点,平行于$AB$的直线为$x$轴,建立平面直角坐标系,可求抛物线相应的函数表达式为$y = -1.1x^{2}$,当$x = 1.2$时,$y = -1.584$,$4.4 - 1.584 = 2.816 > 2.8$,所以能通过
解析:
以顶点$C$为原点,平行于$AB$的直线为$x$轴,建立平面直角坐标系。由题意知,点$A(-2, -4.4)$,$B(2, -4.4)$。设抛物线函数表达式为$y = ax^{2}$,将$B(2, -4.4)$代入得$-4.4 = a × 2^{2}$,解得$a = -1.1$,故抛物线表达式为$y = -1.1x^{2}$。当$x = 1.2$时,$y = -1.1×(1.2)^{2} = -1.584$。此时货物顶部距地面高度为$4.4 - |-1.584| = 2.816\ m$,因为$2.816 > 2.8$,所以这辆汽车能顺利通过该大门。
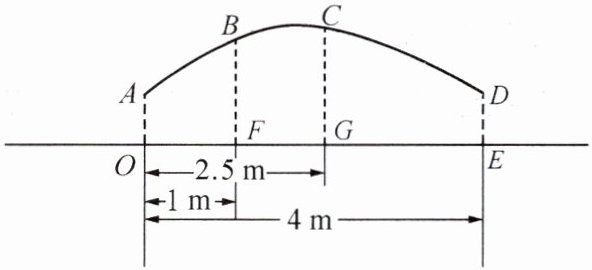
在跳大绳时,假设绳甩到最高处时的形状可近似看作抛物线形. 如图,正在甩绳的两人之间的距离 OE 为 4 m,手部到地面的距离 AO、DE 均为 1 m,跳绳的甲、乙两人与左侧甩绳人之间的距离 OF、OG 分别为 1 m、2.5 m,绳甩到最高处时,刚好通过他们的头顶. 已知甲的身高 BF 为 1.5 m,求乙的身高 CG.
答案:解:以顶点C为原点,平行于AB的直线为x轴,建立平面直角坐标系
则抛物线经过点(0,0)、(2,-4.4)、(-2,-4.4)
设抛物线表达式为y= ax²
将点(2,-4.4)代入表达式得
a=-1.1
∴抛物线的表达式为y= - 1.1x²
当x=1.2时,$y=-1.1×(1.2)²=2.816\gt 2.8$
∴能通过
答:这辆汽车能顺利通过大门。
解:以甲甩绳的手所在垂直方向为y轴坐标原点,
地面所在水平方向为x轴,建立平面直角坐标系。
抛物线经过点(0,1)、(1,1.5)、(4,1)
设抛物线的表达式为y= ax²+ bx +c
$\begin{cases}{c=1 }\\{a+b+c=1.5} \\{16a+4b+c=1} \end{cases}\ \ \ \ \ $解得$\begin{cases}{a=-\dfrac {1}{6}}\\{b=\dfrac {2}{3}}\\{c=1}\end{cases}$
∴抛物线表达式为$y= -\frac {1}{6}x²+\frac {2}{3}x+1$
当x=2.5时,y=1.625
答:学生乙的身高为1.625m。