1. 两个一次函数图象的交点意味着当自变量取某个数值时,两个函数值
相等
.
答案:相等
2. 解决与函数图象相关的实际问题,关键是从图象中获取解题信息,这是
数形结合
思想的具体体现.
答案:数形结合
1. 甲、乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y(km)与时刻t的对应关系如图所示,则下列结论错误的是 (
D
)
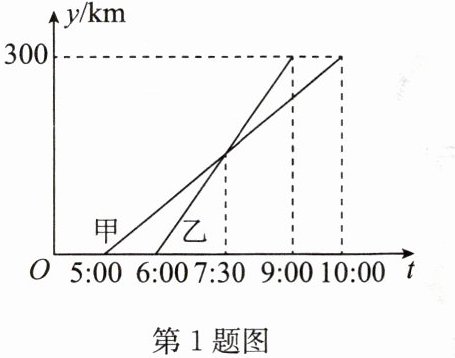
A.甲车的平均速度为60 km/h
B.乙车的平均速度为100 km/h
C.乙车比甲车先到B城
D.乙车比甲车先出发1 h
答案:D
解析:
A.甲车行驶时间:$10:00 - 5:00 = 5\ h$,平均速度:$\frac{300}{5} = 60\ km/h$,正确;
B.乙车行驶时间:$9:00 - 6:00 = 3\ h$,平均速度:$\frac{300}{3} = 100\ km/h$,正确;
C.乙车$9:00$到达,甲车$10:00$到达,乙车先到,正确;
D.甲车$5:00$出发,乙车$6:00$出发,甲车比乙车先出发$1\ h$,错误。
结论错误的是D。
2. 我国很多城市水资源匮乏,为了加强居民的节水意识,某自来水公司采取分段收费方式.某市居民月缴水费y(元)与用水量$x(m^3)$之间的关系如图所示.若某户居民4月份用水$20 m^3,$则应缴水费
44
元.
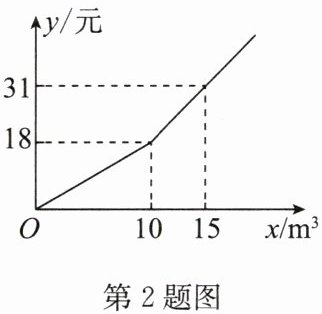
答案:44
解析:
解:当$x \leq 10$时,设$y = kx$,将$(10, 18)$代入得$10k = 18$,解得$k = 1.8$,即$y = 1.8x$。
当$x > 10$时,设$y = ax + b$,将$(10, 18)$,$(15, 31)$代入得$\begin{cases}10a + b = 18 \\ 15a + b = 31\end{cases}$,解得$\begin{cases}a = 2.6 \\ b = -8\end{cases}$,即$y = 2.6x - 8$。
当$x = 20$时,$y = 2.6×20 - 8 = 44$。
44
3. 某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示.
(1)求甲、乙两种收费方式的函数表达式;
(2)该校某年级每次需印制320~350份学案,选择哪种收费方式较合算?
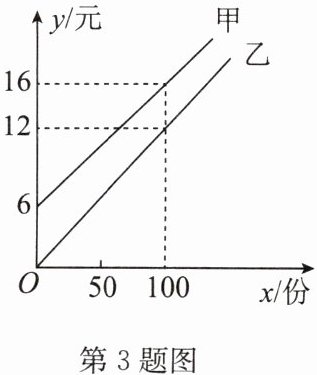
答案:3. 解:
(1)设甲种收费方式的函数表达式是$y_{1}=kx+b$,乙种收费方式的函数表达式是$y_{2}=k'x.$
把$(0,6),(100,16)$代入$y_{1}=kx+b$,得
$\left\{\begin{array}{l} b=6,\\ 100k+b=16,\end{array}\right. $解得$\left\{\begin{array}{l} k=0.1,\\ b=6,\end{array}\right. $
$\therefore y_{1}=0.1x+6$(x 为正整数).
把$(100,12)$代入$y_{2}=k'x$,解得$k'=0.12,$
$\therefore y_{2}=0.12x$(x 为正整数).
(2)由题意,得
当$y_{1}>y_{2}$时,$0.1x+6>0.12x$,解得$x<300;$
当$y_{1}=y_{2}$时,$0.1x+6=0.12x$,解得$x=300;$
当$y_{1}<y_{2}$时,$0.1x+6<0.12x$,解得$x>300.$
∴当x在320~350范围时,选择甲种收费方式较合算.