2. 等边三角形的性质定理:等边三角形的各角都等于
60°
.
答案:60°
3. 等边三角形的判定定理:
(1)三个角都
相等
的三角形是等边三角形.
(2)有一个角是 $60^{\circ}$ 的
等腰
三角形是等边三角形.
答案:
(1)相等
(2)等腰
4. 在直角三角形中,如果一个锐角等于 $30^{\circ}$,那么它所对的直角边是斜边的
一半
.
答案:一半
1. 在 $Rt\triangle ABC$ 中,$\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$,$AB = 6\ cm$,则 $AC$ 的长度为 (
B
)
A.$2\ cm$
B.$3\ cm$
C.$6\ cm$
D.$12\ cm$
答案:B
解析:
在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,$\angle B=30^{\circ}$,$AB=6\ cm$。
因为在直角三角形中,$30^{\circ}$角所对的直角边等于斜边的一半,$\angle B$所对的直角边为$AC$,斜边为$AB$,
所以$AC=\frac{1}{2}AB=\frac{1}{2}×6=3\ cm$。
B
2. 在等边三角形中,两条中线所夹的锐角的度数为 (
D
)
A.$30^{\circ}$
B.$40^{\circ}$
C.$50^{\circ}$
D.$60^{\circ}$
答案:D
解析:
设等边三角形为$ABC$,中线$AD$、$BE$交于点$O$。
$\because \triangle ABC$是等边三角形,
$\therefore \angle BAC = 60°$,$AD$、$BE$分别平分$\angle BAC$、$\angle ABC$,
$\therefore \angle BAD = \frac{1}{2}\angle BAC = 30°$,$\angle ABE = \frac{1}{2}\angle ABC = 30°$。
在$\triangle AOB$中,$\angle AOB = 180° - \angle BAD - \angle ABE = 180° - 30° - 30° = 120°$,
$\therefore$两条中线所夹锐角为$180° - 120° = 60°$。
D
3. 如图,在等边三角形 $ABC$ 中,$DE// BA$ 分别交 $BC$,$AC$ 于点 $D$,$E$. 求证:$\triangle CDE$ 是等边三角形.
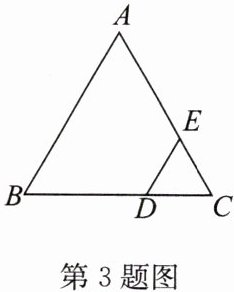
答案:证明:
∵△ABC 是等边三角形,
∴∠A=∠B=∠C=60°.
∵DE//BA,
∴∠CED=∠A=60°,∠CDE=∠B=60°.
∴∠CDE=∠CED=∠C.
∴△CDE 是等边三角形.
4. 如图,在等边$\triangle ABC$ 中,$M$ 是 $BC$ 的中点,$MN\perp AB$,垂足为 $N$,连接 $AM$,求证:$AM = 2MN$.
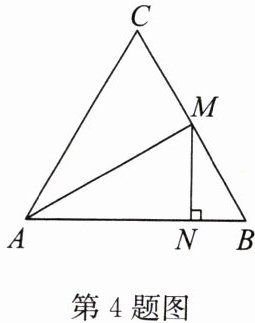
答案:证明:
∵△ABC 是等边三角形,
∴∠BAC=60°,AB=AC.
∵M 是 BC 的中点,
∴∠BAM= $\frac{1}{2}$∠BAC=30°.
又
∵MN⊥AB,
∴AM=2MN.