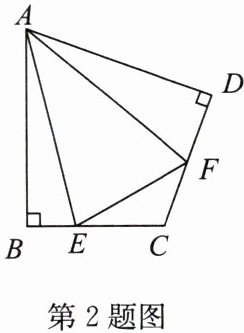
2. 如图,在四边形 $ABCD$ 中,$AB = AD$,$\angle B= \angle D = 90^{\circ}$,$E$,$F$ 分别是边 $BC$,$CD$ 上的点,$\angle EAF= \frac{1}{2}\angle BAD$.
(1) 求证:$EF = BE + FD$;
(2) 求证:$FA$ 平分$\angle DFE$.
答案:(1)如答图,延长EB至点G,使BG=DF,连接AG.
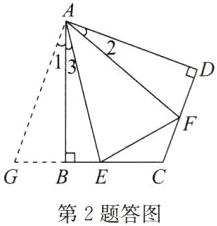
在△ABG和△ADF中,$\left\{\begin{array}{l} AB=AD,\\ ∠ABG=∠D=90^{\circ },\\ BG=DF,\end{array}\right. $
∴△ABG≌△ADF(SAS).
∴∠1=∠2,AF=AG.
∵∠EAF=$\frac {1}{2}$∠BAD,
∴∠2+∠3=$\frac {1}{2}$∠BAD=∠1+∠3=∠EAG.
∴∠EAF=∠EAG.又
∵AE=AE,
∴△AEG≌△AEF(SAS).
∴EF=EG,∠G=∠AFE.
∵EG=BE+BG=BE+DF,
∴EF=BE+FD.
(2)
∵△ABG≌△ADF,
∴∠G=∠AFD.又
∵∠G=∠AFE,
∴∠AFE=∠AFD.
∴FA平分∠DFE.