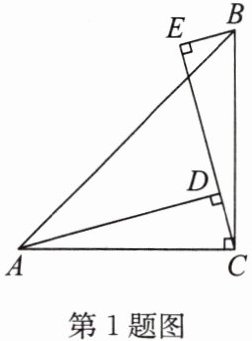
1. 如图,$\angle ACB= 90^{\circ}$,$AC= BC$,$AD\perp CE$,$BE\perp CE$,垂足分别是$D$,$E$,$AD= 3$,$BE= 1$,则$DE$的长为(
B
)
A.1.5
B.2
C.2.4
D.2.5
答案:B 点拨:
∵AD⊥CE,BE⊥CE,
∴∠ADC=∠E=90°.
∵∠ACB=90°,
∴∠ACD+∠BCE=∠BCE+∠EBC=90°,
∴∠ACD=∠EBC. 又
∵AC=CB,
∴△ADC≌△CEB(AAS).
∴CE=AD=3,CD=BE=1.
∴DE=CE-CD=3-1=2. 故选B.
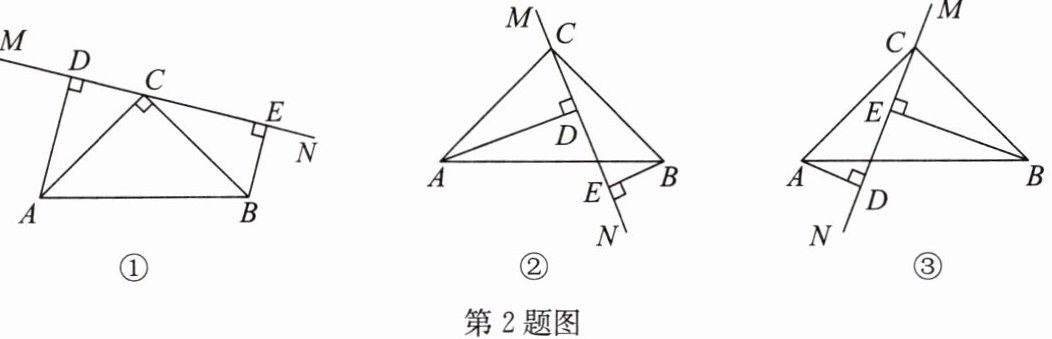
2. 在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,$AC= BC$,直线$MN经过点C$,且$AD\perp MN于点D$,$BE\perp MN于点E$.
(1)当直线$MN$在图①的位置时,填空:
①$\triangle ADC和\triangle CEB$的关系是
△ADC≌△CEB
;
②线段$DE$,$AD和BE$三者之间的数量关系是
DE=AD+BE
.
(2)当直线$MN$在图②的位置时,求证:$DE= AD-BE$.
(3)当直线$MN$在图③的位置时,若$BE= 3$,$AD= 1$,求$DE$的长.
答案:
(1)①△ADC≌△CEB ②DE=AD+BE
(2)证明:
∵∠ACB=90°,AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=∠ACB=90°.
∴∠ACD=∠CBE.在△ADC和△CEB中,∠ADC=∠CEB,∠ACD=∠CBE,AC=CB,
∴△ADC≌△CEB(AAS).
∴CE=AD,CD=BE,
∴DE=CE-CD=AD-BE.
(3)解:由
(2)知△ACD≌△CBE,
∴CD=BE=3,CE=AD=1,
∴DE=CD-CE=3-1=2.