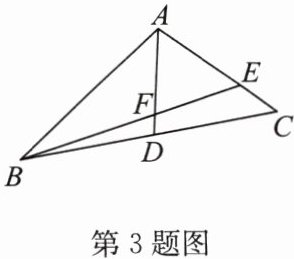
3. 如图,在△ABC 中,BD = CD,BE 交 AD 于点 F,AE = EF. 若 BE = 7CE,AE = $\frac{5}{2}$,求 BF 的长.
答案:3. 解:如答图,延长 AD 至点 G,使 DG=AD,连接 BG.
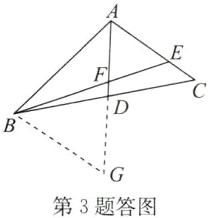
在△BDG 和△CDA 中,$\left\{\begin{array}{l} BD=CD,\\ ∠BDG=∠CDA,\\ GD=AD,\end{array}\right. $
∴△BDG≌△CDA(SAS).
∴BG=AC,∠CAD=∠G.
又
∵AE=EF,
∴∠CAD=∠AFE.
又
∵∠BFG=∠AFE,
∴∠G=∠BFG,
∴BG=BF,
∴AC=BF.
∵BE=7CE,AE=$\frac{5}{2}$,
∴BF+EF=BE=7(AC - AE),
即 BF+$\frac{5}{2}$=7($BF-\frac{5}{2}$),
∴BF=$\frac{10}{3}$.