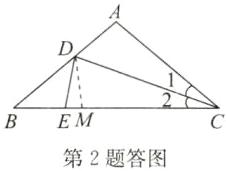
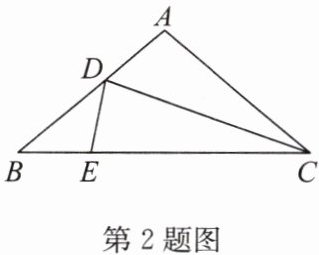
2. 如图,在 $ △ABC $ 中,$ AB = AC $,$ ∠A = 100° $,CD 平分 $ ∠ACB $ 交 AB 于点 D,E 为 BC 边上一点,且 $ BE = DE $,则 AD,BC,CD 三条线段之间的数量关系为______.
答案:2.BC=AD+CD 点拨:如答图,在BC边上取点M,使CM=CA,连接DM,易证△ACD≌△MCD(SAS).
∴∠DMC=∠A=100°,DM=AD.
∵AB=AC,∠A=100°,
∴∠B=∠ACB=40°.
∵CD平分∠ACB,
∴∠1=∠2=20°.
∴∠ADC=180°−∠A−∠1=60°.
∵BE=DE,
∴∠EDB=∠B=40°.
∴∠CED=∠B+∠EDB=80°.
∵∠CDE=180°−∠BDE−∠ADC=80°,
∴∠CDE=∠CED,
∴CE=CD.
∵∠DME=180°−∠DMC=180°−∠A=80°=∠DEM
∴DM=DE=BE.
∵BC=BE+CE,
∴BC=AD+CD.