2025年启东中学作业本八年级数学上册苏科版宿迁专版第152页解析答案

9. (12 分)$ \triangle ABC $ 的三边长分别是 $ a $,$ b $,$ c $,且 $ a = n^{2} - 1 $,$ b = 2n $,$ c = n^{2} + 1 $.
(1) 判断 $ \triangle ABC $ 的形状,并说明理由；
(2) 若以 $ b $ 为直径的半圆的面积为 $ 2\pi $,求 $ \triangle ABC $ 的面积.

答案：
(1)△ABC是直角三角形,理由如下:
∵a=n²-1,b=2n,c=n²+1,
∴a²+b²=(n²-1)²+(2n)²=n⁴-2n²+1+4n²=(n²+1)²,c²=(n²+1)²,
∴a²+b²=c²,
∴△ABC是直角三角形.　
(2)由题意,得$\frac{1}{2}\pi\cdot\left(\frac{b}{2}\right)^2=2\pi$,
∴b=4或b=-4(舍去),
∴2n=4,
∴n=2,
∴a=n²-1=3,
∴△ABC的面积=$\frac{1}{2}ab=\frac{1}{2}×3×4=6$.

10. (14 分)数学老师在黑板上写了一道题：“已知 $ AD $ 是等腰三角形 $ ABC $ 的腰 $ BC $ 上的高,且 $ \angle DAB = 60^{\circ} $.”要求学生画出符合条件的图形,并求出 $ \triangle ABC $ 各角的度数. 小明同学画出的图形如图所示,并在图形中标出 $ \triangle ABC $ 各角的度数. 请你画出所有符合条件且不同于小明同学的图形,并标出 $ \triangle ABC $ 各角的度数.

答案：
解:如答图所示.　　　　　

11. (18 分)如图①,在平面直角坐标系中,已知一次函数 $ y = -x + 6 $ 的图象与 $ x $ 轴、$ y $ 轴分别交于点 $ A $,$ B $.
(1) 求出点 $ A $,$ B $ 的坐标.
(2) $ D $ 是直线 $ AB $ 上的动点,当 $ S_{\triangle AOD} = \frac{1}{2}S_{\triangle ABO} $ 时,求点 $ D $ 的坐标.
(3) 如图②,$ P $ 为 $ A $ 点右侧 $ x $ 轴上的一动点,以 $ P $ 为直角顶点,$ BP $ 为腰在第一象限内作等腰直角 $ \triangle BPQ $,连接 $ QA $ 并延长交 $ y $ 轴于点 $ K $. 当 $ P $ 点运动时,$ K $ 点的位置是否发生变化？如果不变,请求出它的坐标；如果变化,请说明理由.

答案：

(1)在y=-x+6中,令x=0,得y=6;令y=0,得x=6,故A(6,0),B(0,6).　
(2)设D(m,-m+6),由S△AOD=$\frac{1}{2}$S△ABO,得|-m+6|=$\frac{1}{2}$OB,即|-m+6|=3,解得m=3或9,
∴点D的坐标为(3,3)或(9,-3).　
(3)不变.解法一:设P(t,0)(t＞6),如答图，过点Q作QM⊥x轴于点M,则∠QMP=∠POB=90°.
∵△BPQ是等腰直角三角形，
∴PB=PQ,∠BPQ=90°.
∴∠OPB+∠QPM=∠PQM+∠QPM=90°.
∴∠OPB=∠PQM,
∴△POB≌△QMP(AAS),
∴PM=OB=6,MQ=OP=t,
∴Q(t+6,t).　设直线AQ的函数表达式为y=kx+b,　则$\begin{cases}6k+b=0,\\(t+6)k+b=t,\end{cases}$解得$\begin{cases}k=1,\\b=-6.\end{cases}$
∴直线AQ的函数表达式为y=x-6,交y轴于点(0,-6),
∴K(0,-6).　　　　　　　

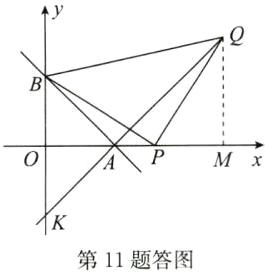
　解法二:由解法一可知PM=OB=OA,
　
∴OA+AP=PM+AP,即OP=AM.　又
∵QM=OP,
　
∴AM=MQ,
∴△AMQ是等腰直角三角形,
　
∴无论点P如何运动，QA与x轴的正半轴的夹角都为45°,
∴△AOK是等腰直角三角形，
∴K(0,-6).