19. (6分)已知一次函数$ y = ( 2 a - 1 ) x + a - 2 $.
(1)若这个函数是正比例函数,求a的值;
(2)若这个函数的图象经过第一、三、四象限,求a的取值范围.
答案:解:
(1)
∵y=(2a−1)x+a−2是正比例函数,
∴a−2=0且2a−1≠0,解得a=2,
∴a的值为2.
(2)
∵一次函数y=(2a−1)x+a−2的图象经过第一、三、四象限,
∴$\begin{cases}2a - 1 > 0 \\ a - 2 < 0 \end{cases}$,解得$\frac{1}{2}$<a<2,
∴a的取值范围为$\frac{1}{2}$<a<2.
20. (6分)已知一次函数的图象经过点$ A ( 1, 1 ) $,$ B ( - 1, - 3 ) $.
(1)求此一次函数的表达式;
(2)求此一次函数的图象与两坐标轴围成的三角形面积.
答案:解:
(1)设此一次函数的表达式为y=kx+b,将(1,1),(−1,−3)代入,得$\begin{cases}k + b = 1 \\ -k + b = -3 \end{cases}$,解得$\begin{cases}k = 2 \\ b = -1 \end{cases}$.
∴此一次函数的表达式为y=2x−1.
(2)在y=2x−1中,令x=0,得y=−1;令y=0,得x=$\frac{1}{2}$,
∴令直线y=2x−1交x轴于点M($\frac{1}{2}$,0),交y轴于点N(0,−1),从而OM=$\frac{1}{2}$,ON=1.
∴S$_{\triangle MON}$=$\frac{1}{2}$OM·ON=$\frac{1}{2}$×$\frac{1}{2}$×1=$\frac{1}{4}$,即此一次函数的图象与两坐标轴围成的三角形面积为$\frac{1}{4}$.
21. (6分)在平面直角坐标系xOy中,已知点$ A ( - 1, 2 ) $,$ B ( 0, 4 ) $,$ C ( 3, 10 ) $. 求证:A,B,C三点在同一条直线上.
答案:证明:设直线AB的函数表达式为y=kx+b,则$\begin{cases}-k + b = 2 \\ b = 4 \end{cases}$,解得$\begin{cases}k = 2 \\ b = 4 \end{cases}$,
∴直线AB的函数表达式为y=2x+4.在y=2x+4中,当x=3时,y=10,
∴点C(3,10)在直线AB上,
∴A,B,C三点在同一条直线上.
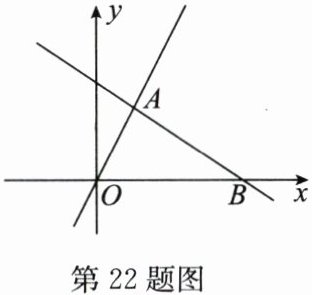
22. (8分)如图,已知一次函数$ y = k x + b 的图象过点 ( - 2, 4 ) $,与正比例函数$ y = 2 x 的图象交于点 A ( 1, a ) $.
(1)求一次函数的表达式;
(2)若直线$ y = k x + b $与x轴交于点B,求$ S _ { \triangle A O B } $.
答案:解:
(1)
∵正比例函数y=2x的图象过点A(1,a),
∴a=2×1=2,
∴A(1,2).
∵一次函数y=kx+b的图象过点(−2,4),(1,2),
∴$\begin{cases}-2k + b = 4 \\ k + b = 2 \end{cases}$,解得$\begin{cases}k = -\frac{2}{3} \\ b = \frac{8}{3} \end{cases}$.
∴一次函数的表达式为y=−$\frac{2}{3}$x+$\frac{8}{3}$.
(2)
∵直线y=−$\frac{2}{3}$x+$\frac{8}{3}$与x轴交于点B(4,0),
∴OB=4,
∴S$_{\triangle AOB}$=$\frac{1}{2}$OB·|y$_A$|=$\frac{1}{2}$×4×2=4.