2025年启东中学作业本八年级数学上册苏科版宿迁专版第94页解析答案

1. 已知点 $ P(1 + m,3) $ 在第二象限,则 $ m $ 的取值范围是(

)
A.$ m \leq -1 $
B.$ m ＞ -1 $
C.$ m ＜ -1 $
D.$ m \geq -1 $

答案：C

解析：

因为点$P(1 + m,3)$在第二象限，第二象限内点的横坐标小于$0$，所以$1 + m ＜ 0$，解得$m ＜ -1$。
C

2. (2024·通辽)剪纸是我国民间艺术之一,如图放置的剪纸作品,它的对称轴与平面直角坐标系的坐标轴重合,则点 $ A(-4,2) $ 关于对称轴对称的点的坐标为(

)

A.$ (-4,-2) $
B.$ (4,-2) $
C.$ (4,2) $
D.$ (-2,-4) $

答案：C

解析：

解：由图可知，剪纸作品的对称轴为y轴。
点$A(-4,2)$关于y轴对称的点的坐标为$(4,2)$。
答案：C

3. (2024·包头)如图,在平面直角坐标系中,四边形 $ OABC $ 各顶点的坐标分别是 $ O(0,0) $,$ A(1,2) $,$ B(3,3) $,$ C(5,0) $,则四边形 $ OABC $ 的面积为(

)

A.14
B.11
C.10
D.9

答案：D

解析：

解：过点A作AD⊥x轴于D，过点B作BE⊥x轴于E。
∵A(1,2)，B(3,3)，C(5,0)，
∴OD=1，AD=2，DE=3-1=2，BE=3，EC=5-3=2。
S=S△OAD+S梯形ADEB+S△BEC
= $\frac{1}{2}×1×2+\frac{1}{2}×(2+3)×2+\frac{1}{2}×2×3$
=1+5+3=9。
答案：D

4. 如图,点 $ A(-1,0) $,点 $ B(0,2) $,线段 $ AB $ 平移后得到线段 $ A'B' $。若点 $ A'(2,a) $,点 $ B'(b,1) $,则 $ a - b $ 的值是(

)

A.-4
B.-2
C.2
D.4

答案：A

解析：

解：由点$A(-1,0)$平移到$A'(2,a)$，横坐标变化为$2 - (-1) = 3$，故平移规律为向右平移3个单位。
由点$B(0,2)$平移到$B'(b,1)$，纵坐标变化为$1 - 2 = -1$，故平移规律为向下平移1个单位。
综上，线段$AB$先向右平移3个单位，再向下平移1个单位得到线段$A'B'$。
则$a = 0 - 1 = -1$，$b = 0 + 3 = 3$。
$a - b = -1 - 3 = -4$
答案：A

5. 在平面直角坐标系中,已知点 $ A(0,3) $,$ B(2,1) $,经过点 $ A $ 的直线 $ l // x $ 轴,$ C $ 是直线 $ l $ 上的一个动点,当线段 $ BC $ 的长度最短时,点 $ C $ 的坐标为(

)
A.$ (0,1) $
B.$ (2,0) $
C.$ (2,-1) $
D.$ (2,3) $

答案：D

解析：

∵直线$l// x$轴且过点$A(0,3)$，
∴直线$l$的解析式为$y = 3$。
∵点$C$是直线$l$上的动点，
∴设点$C$的坐标为$(x,3)$。
∵点$B$的坐标为$(2,1)$，
∴线段$BC$的长度为$\sqrt{(x - 2)^2+(3 - 1)^2}=\sqrt{(x - 2)^2 + 4}$。
∵$(x - 2)^2\geq0$，
∴当$x = 2$时，$BC$的长度最短，此时点$C$的坐标为$(2,3)$。
D

6. 若点 $ P(a,b) $ 在第四象限,且到 $ x $ 轴的距离为 5,到 $ y $ 轴的距离 3,则 $ a + b = $

-2

。

答案：-2

解析：

点$P(a,b)$在第四象限，所以$a＞0$，$b＜0$。
点$P$到$x$轴的距离为$5$，则$|b|=5$，又因为$b＜0$，所以$b=-5$。
点$P$到$y$轴的距离为$3$，则$|a|=3$，又因为$a＞0$，所以$a=3$。
因此，$a + b=3+(-5)=-2$。
$-2$

7. 在平面直角坐标系中,点 $ A(2,3) $ 关于 $ x $ 轴对称的点的坐标是

(2,-3)

。

答案：(2,-3)

8. (2024·湖滨新区期末)将点 $ A(-3,-1) $ 先向左平移 2 个单位长度,再向上平移 4 个单位长度,得到点 $ A' $,则点 $ A' $ 的坐标为

(-5,3)

。

答案：(-5,3)

解析：

点$A(-3,-1)$向左平移2个单位长度，横坐标变为$-3-2=-5$；再向上平移4个单位长度，纵坐标变为$-1+4=3$，所以点$A'$的坐标为$(-5,3)$。

9. 画一条水平数轴,以原点 $ O $ 为圆心,过数轴上的每一刻度点画同心圆,过原点 $ O $ 按逆时针方向依次画出与正半轴的角度分别为 $ 30^{\circ} $,$ 60^{\circ} $,$ 90^{\circ} $,$ 120^{\circ} $,…,$ 330^{\circ} $ 的射线,这样就建立了“圆”坐标系。如图,在建立的“圆”坐标系内,我们可以将点 $ A $,$ B $,$ C $ 的坐标分别表示为 $ A(6,60^{\circ}) $,$ B(5,180^{\circ}) $,$ C(4,330^{\circ}) $,则点 $ D $ 的坐标可以表示为______。

(3,150°)

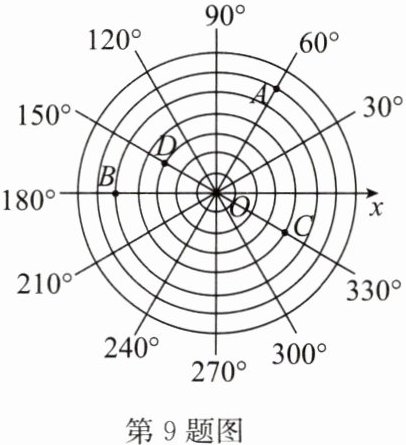
答案：(3,150°)