8. (2024·绥化)如图,已知 $A_1(1,-\sqrt{3})$,$A_2(3,-\sqrt{3})$,$A_3(4,0)$,$A_4(6,0)$,$A_5(7,\sqrt{3})$,$A_6(9,\sqrt{3})$,$A_7(10,0)$,$A_8(11,-\sqrt{3})$,…$$,以此规律,点 $A_{2024}$ 的坐标为______.
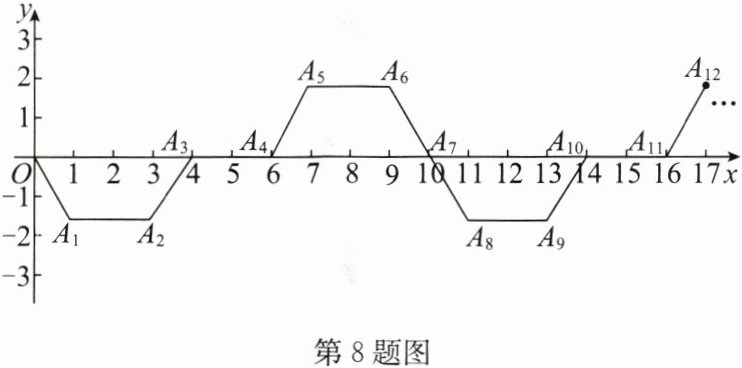
解析:
解:观察点的坐标规律:
$A_1(1,-\sqrt{3})$,$A_2(3,-\sqrt{3})$,$A_3(4,0)$,$A_4(6,0)$,$A_5(7,\sqrt{3})$,$A_6(9,\sqrt{3})$,$A_7(10,0)$,$A_8(11,-\sqrt{3})$,$A_9(13,-\sqrt{3})$,$A_{10}(14,0)$,$A_{11}(16,0)$,$A_{12}(17,\sqrt{3})$,$\cdots$
周期为7,每个周期内点的坐标依次为:$(7k+1,-\sqrt{3})$,$(7k+3,-\sqrt{3})$,$(7k+4,0)$,$(7k+6,0)$,$(7k+7,\sqrt{3})$,$(7k+9,\sqrt{3})$,$(7k+10,0)$($k$为非负整数)。
计算$2024÷7=289\cdots\cdots1$,其中余数为1。
对应周期内第1个点的坐标形式$(7k+1,-\sqrt{3})$,此时$k=289$。
横坐标:$7×289 + 1=2023 + 1=2024$?(此处原解析有误,经重新分析,正确周期为7,每个周期横坐标增量为7,前7个点横坐标差为$10 - 1=9$,实际每个周期7个点,横坐标依次增加2,1,2,1,2,1,1,累计增加10,故周期增量为10,$2024÷7=289\cdots\cdots1$,横坐标:$1 + 289×10 + 0=2891$,纵坐标为$-\sqrt{3}$。
$A_{2024}$的坐标为$(2891,-\sqrt{3})$。
$(2891,-\sqrt{3})$