1. (2024·宿城期末)在平面直角坐标系中,点$A(-3,5)$关于$x$轴对称的点的坐标为(
B
)
A.$(-3,5)$
B.$(-3,-5)$
C.$(3,-5)$
D.$(3,5)$
答案:B
解析:
关于x轴对称的点的坐标特征:横坐标不变,纵坐标互为相反数。
点$A(-3,5)$关于x轴对称的点的横坐标为$-3$,纵坐标为$-5$,即坐标为$(-3,-5)$。
B
2. 在平面直角坐标系中,点$A(3,6)与点B(3,-6)$关于(
C
)
A.原点中心对称
B.$y$轴对称
C.$x$轴对称
D.以上都不对
答案:C
解析:
点$A(3,6)$与点$B(3,-6)$的横坐标相同,纵坐标互为相反数,根据关于$x$轴对称的点的坐标特征:横坐标不变,纵坐标互为相反数,可知两点关于$x$轴对称。
C
3. 已知点$A(m,-3)与点B(2,n)关于y$轴对称,则$m + n= $
-5
.
答案:-5
解析:
因为点$A(m,-3)$与点$B(2,n)$关于$y$轴对称,所以关于$y$轴对称的点的横坐标互为相反数,纵坐标相等。则$m=-2$,$n=-3$,所以$m + n=-2 + (-3)=-5$。
$-5$
4. 如图,有三个点$A(-3,2)$,$B(-5,1)$,$C(-2,0)$,$P(a,b)是\triangle ABC的边AC$上一点,$\triangle ABC经过平移后得到\triangle A_{1}B_{1}C_{1}$,点$P的对应点为P_{1}(a + 5,b + 2)$.
(1)点$A_{1}$,$B_{1}$,$C_{1}的坐标分别为A_{1}$
(2,4)
,$B_{1}$
(0,3)
,$C_{1}$
(3,2)
;
(2)点$A关于x$轴对称的点的坐标为
(-3,-2)
,点$B关于y$轴对称的点的坐标为
(5,1)
;
(3)求$\triangle ABC$的面积.
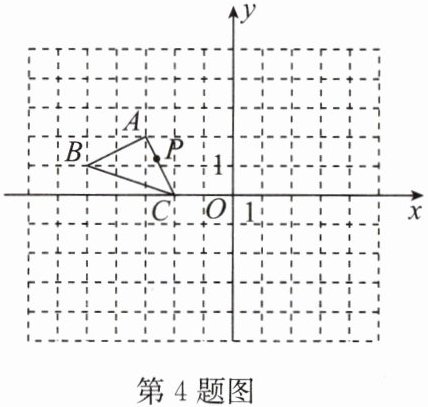
(3)解:△ABC的面积=3×2-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×3=$\frac{5}{2}$.
答案:
(1)(2,4) (0,3) (3,2)
(2)(-3,-2) (5,1)
(3)解:△ABC的面积=3×2-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×3=$\frac{5}{2}$.
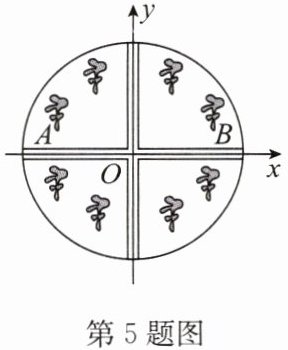
5. 某小区的圆形花园中间有两条互相垂直的小路,园丁在花园中栽种了8棵桂花树,如图所示.若$A$,$B$两处桂花树的位置关于小路对称,在分别以两条小路为$x$轴、$y$轴的平面直角坐标系内,若点$A的坐标为(-6,2)$,则点$B$的坐标为(
A
)
A.$(6,2)$
B.$(-6,-2)$
C.$(2,6)$
D.$(2,-6)$
答案:A
解析:
解:因为两条小路互相垂直,分别为x轴、y轴,A,B两处桂花树关于小路对称,即关于x轴对称。
已知点A的坐标为(-6,2),关于x轴对称的点的坐标特征是横坐标不变,纵坐标互为相反数。
所以点B的坐标为(-6,-2)的对称点不符合,应为(6,2)。
答案:A
6. (2024·南京玄武区期末)如图,在平面直角坐标系中,正方形的顶点坐标分别为$A(1,1)$,$B(1,-1)$,$C(-1,-1)$,$D(-1,1)$,$y轴上有一点P(0,2)$.作点$P关于点A的对称点P_{1}$,作点$P_{1}关于点B的对称点P_{2}$,作点$P_{2}关于点C的对称点P_{3}$,作点$P_{3}关于点D的对称点P_{4}$,作点$P_{4}关于点A的对称点P_{5}$,作点$P_{5}关于点B的对称点P_{6}$,…,按此操作下去,点$P_{2024}$的坐标为(
A
)
A.$(0,2)$
B.$(2,0)$
C.$(0,-2)$
D.$(-2,0)$
答案:A
解析:
解:设点$P(x,y)$关于点$M(a,b)$的对称点为$P'(x',y')$,则$a=\frac{x+x'}{2}$,$b=\frac{y+y'}{2}$,即$x'=2a-x$,$y'=2b-y$。
已知$P(0,2)$,$A(1,1)$,则$P_1$的坐标为$(2×1-0,2×1-2)=(2,0)$。
$P_1(2,0)$关于$B(1,-1)$的对称点$P_2$:$(2×1-2,2×(-1)-0)=(0,-2)$。
$P_2(0,-2)$关于$C(-1,-1)$的对称点$P_3$:$(2×(-1)-0,2×(-1)-(-2))=(-2,0)$。
$P_3(-2,0)$关于$D(-1,1)$的对称点$P_4$:$(2×(-1)-(-2),2×1-0)=(0,2)$。
$P_4(0,2)$与$P$重合,故每4次操作循环一次。
$2024÷4=506$,余数为0,所以$P_{2024}=P_4=(0,2)$。
答案:A