1. 如图,在一次“寻宝”游戏中,寻宝人已经找到两个标志点 $ A(-1,2) $ 和 $ B(2,1) $,则藏宝处点 $ C $ 的坐标应为(
A
)
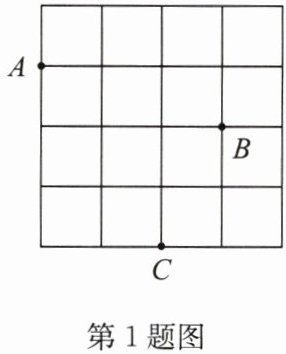
A.$ (1,-1) $
B.$ (1,0) $
C.$ (-1,1) $
D.$ (0,1) $
答案:A
解析:
以点$A(-1,2)$为基准,观察网格中各点位置关系,通过坐标平移规律可得点$C$的坐标为$(1,-1)$。
A
2. 中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱. 如图,在象棋棋盘上建立平面直角坐标系,若“馬”的坐标为 $ (1,3) $,“車”的坐标为 $ (-2,3) $,则“炮”的坐标为(
C
)
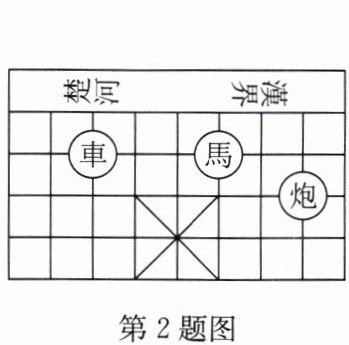
A.$ (2,3) $
B.$ (2,2) $
C.$ (3,2) $
D.$ (4,2) $
答案:C
解析:
根据“馬”的坐标$(1,3)$和“車”的坐标$(-2,3)$,可知两点在同一水平线上,距离为$1 - (-2) = 3$个单位长度,对应棋盘上3列。由此确定坐标原点位置,进而得出“炮”的坐标为$(3,2)$。
C
3. 一个正方形在平面直角坐标系中三个顶点的坐标分别为 $ (0,0) $,$ (0,3) $,$ (3,0) $,则第四个顶点的坐标为
(3,3)
.
答案:(3,3)
4. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ BC = 4 $,$ BC $ 边上的高 $ AD = 4 $,则以点
D
为坐标原点,以
BC
所在的直线为 $ x $ 轴,以
AD
所在的直线为 $ y $ 轴建立的平面直角坐标系较简明,此时 $ A $,$ B $,$ C $ 三个点的坐标依次是
(0,4)
,
(-2,0)
,
(2,0)
.
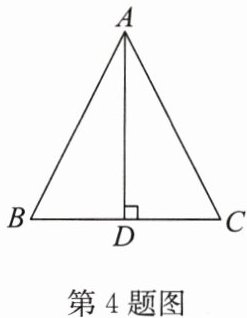
答案:D BC AD (0,4) (-2,0) (2,0)
解析:
D;BC;AD;(0,4);(-2,0);(2,0)
5. 如图是某野生动物世界部分景点的分布示意图,分别以正东、正北方向为 $ x $ 轴、$ y $ 轴的正方向建立平面直角坐标系,并且“五彩广场”和“考拉园”的坐标分别是 $ (-3,1) $ 和 $ (-1,-1) $.
(1) 根据题意,画出正确的平面直角坐标系;
(2) 分别写出“百虎山”“熊猫乐园”的坐标.

答案:解:
(1)平面直角坐标系如答图所示.
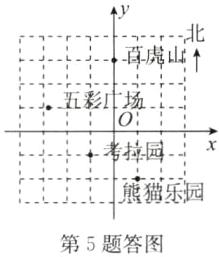
(2)“百虎山”“熊猫乐园”的坐标分别为(0,3),(1,-2).
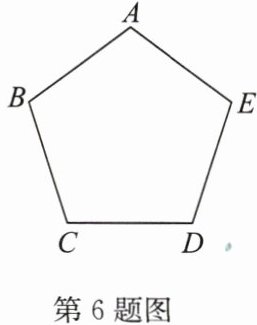
6. 如图,将正五边形 $ ABCDE $ 置于平面直角坐标系中,若顶点 $ A $,$ B $,$ C $,$ D $ 的坐标分别是 $ (0,a) $,$ (-2,-1) $,$ (c,m) $,$ (d,m) $,则第四个顶点的坐标为(
A
)
A.$ (2,-1) $
B.$ (2,1) $
C.$ (-1,-2) $
D.$ (-2,1) $
答案:A
解析:
解:正五边形$ABCDE$中,点$C(d,m)$,$D(d,m)$,则$CD$边平行于$x$轴,且$C$、$D$关于过点$A$的铅垂线对称。
点$A$坐标为$(0,a)$,故对称轴为$y$轴。
已知点$B(-2,-1)$,则其关于$y$轴的对称点为$E(2,-1)$。
答案:A