1.【问题驱动】如何验证勾股定理及探究勾股数?
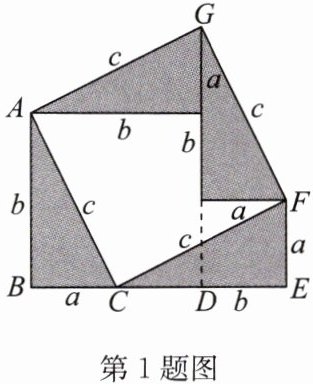
【活动操作】小明用4张全等的直角三角形纸片拼成如图所示的五边形$ ABEFG $.
【探索新知】
(1)从面积的角度思考,请用两种方法计算五边形$ ABEFG $的面积,并写出得到等式$ a^{2}+b^{2}= c^{2} $的过程;
(2)如果满足等式$ a^{2}+b^{2}= c^{2} 的 a,b,c $是三个正整数,我们称$ a,b,c $为勾股数.已知$ m,n 是正整数且 m>n $,证明:$ 2mn,m^{2}-n^{2},m^{2}+n^{2} $是勾股数;
【灵活运用】
(3)在如图所示的五边形$ ABEFG $中,若$ a = 4,b = 8 $,则空白部分的面积为______;
(4)请写出任意一组含有85的“勾股数”:______;
(5)小明在他找到的勾股数的表达式中,用$ 2n^{2}+4n+4 $($ n $为任意正整数)表示勾股数中的最大的一个数,则另外两个数的表达式分别是______、______.
答案:1.
(1)解:如答图所示.
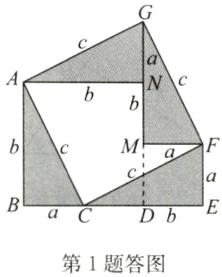
方法一:$S_{五边形ABEF G}=S_{正方形ABDN}+S_{正方形MDEF}+S_{\triangle MFG}+S_{\triangle ANG}$
$=b^{2}+a^{2}+\frac {1}{2}ab+\frac {1}{2}ab$
$=a^{2}+b^{2}+ab.$
方法二:$S_{五边形ABEF G}=S_{正方形ACFG}+S_{\triangle ABC}+S_{\triangle CEF}$
$=c^{2}+\frac {1}{2}ab+\frac {1}{2}ab=c^{2}+ab.$
$\therefore a^{2}+b^{2}+ab=c^{2}+ab,$
$\therefore a^{2}+b^{2}=c^{2}.$
(2)证明:$\because (2mn)^{2}=4m^{2}n^{2},(m^{2}-n^{2})^{2}=m^{4}+n^{4}-2m^{2}n^{2},$
$\therefore (2mn)^{2}+(m^{2}-n^{2})^{2}=4m^{2}n^{2}+m^{4}+n^{4}-2m^{2}n^{2}=(m^{2}+n^{2})^{2}.$
$\because m,n$是正整数且$m>n,$
$\therefore 2mn,m^{2}-n^{2},m^{2}+n^{2}$都是正整数,
$\therefore 2mn,m^{2}-n^{2},m^{2}+n^{2}$是勾股数.
(3)48
(4)85,3612,3613(答案不唯一)
(5)$2n^{2}+4n$ $4n+4$