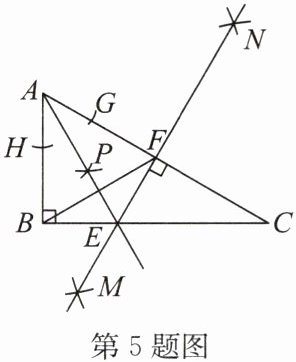
5. (2024·泰安)如图,$Rt\triangle ABC$中,$\angle ABC = 90^{\circ}$,分别以顶点$A,C$为圆心,大
于
$\frac{1}{2}AC$长为半径画弧,两弧分别相交于点$M和点N$,作直线$MN$,分别与$BC,AC交于点E和点F$;以点$A$为圆心,任意长为半径画弧,分别交$AB,AC于点H和点G$,再分别以点$H,G$为圆心,大于$\frac{1}{2}HG$长为半径画弧,两弧交于点$P$,作射线$AP$,若射线$AP恰好经过点E$,则下列四个结论:①$\angle C = 30^{\circ}$;②$AP垂直平分线段BF$;③$CE = 2BE$;④$S_{\triangle BEF}= \frac{1}{6}S_{\triangle ABC}$.其中,正确的结论有 (
D
)
A.1个
B.2个
C.3个
D.4个
解析:
证明:
1. 由作图知,MN垂直平分AC,AP平分∠BAC。设∠BAE=∠CAE=α,则∠BAC=2α,∠C=90°-2α。
∵MN垂直平分AC,
∴EA=EC,∠EAC=∠C=90°-2α。
又∠EAC=α,
∴α=90°-2α,解得α=30°,∠C=30°,①正确。
2.
∵∠BAC=60°,MN垂直平分AC,F为AC中点,BF=AF=CF。
AP平分∠BAC,∠BAE=30°,∠ABC=90°,∠AEB=60°。
∵BF=AF,∠BAF=60°,△ABF为等边三角形,AP⊥BF且平分BF,②正确。
3. 设BE=x,∠BAE=30°,AB=√3 x,AE=2x=EC。
∵∠C=30°,BC=AB·√3=3x,CE=BC-BE=2x,即CE=2BE,③正确。
4. 设BE=x,AB=√3 x,BC=3x,S△ABC=1/2·AB·BC=3√3/2 x²。
F为AC中点,BF=1/2 AC=√3 x,EF=BE=x,S△BEF=1/2·BE·EF·sin60°=√3/4 x²=1/6 S△ABC,④正确。
结论:①②③④均正确,选D。
D