1. 如图,公路 $ AC $,$ BC $ 互相垂直,$ M $ 为公路 $ AB $ 的中点,为测量湖泊两侧 $ C $,$ M $ 两点间的距离,若测得 $ AB $ 的长为 $ 6 km $,则 $ M $,$ C $ 两点间的距离为(
D
)
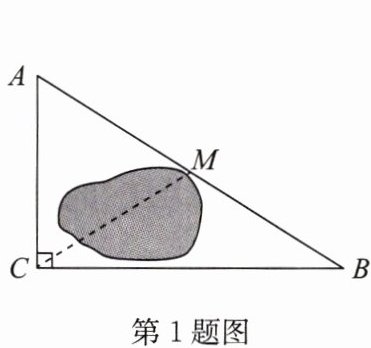
A.$ 2.5 km $
B.$ 4.5 km $
C.$ 5 km $
D.$ 3 km $
答案:D
解析:
解:在$Rt\triangle ABC$中,$\angle ACB=90°$,$M$为斜边$AB$的中点。
根据直角三角形斜边中线定理,斜边中线等于斜边的一半,得$CM=\frac{1}{2}AB$。
已知$AB=6\ km$,则$CM=\frac{1}{2}×6=3\ km$。
答案:D
2. 如图,在 $ Rt \triangle ABC $ 中,斜边 $ AB $ 上的中线 $ CD = 5 $,则 $ AB = $
10
.
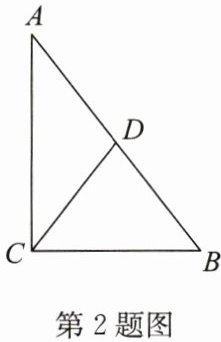
答案:10
解析:
解:在$Rt\triangle ABC$中,$CD$是斜边$AB$上的中线,根据直角三角形斜边中线定理,斜边中线等于斜边的一半,即$CD=\frac{1}{2}AB$。已知$CD = 5$,则$AB=2CD=2×5 = 10$。
$10$
3. 直角三角形斜边上的高与中线分别为 $ 5 cm $ 和 $ 6 cm $,则它的面积为
30
$ cm^2 $.
答案:30
解析:
在直角三角形中,斜边上的中线等于斜边的一半。已知斜边上的中线为$6\,cm$,所以斜边的长为$2×6 = 12\,cm$。
直角三角形的面积可以表示为$\frac{1}{2}×斜边×斜边上的高$,已知斜边上的高为$5\,cm$,则该直角三角形的面积为$\frac{1}{2}×12×5 = 30\,cm^2$。
30
4. (2025·镇江期中)若直角三角形斜边上的高是 $ 4 cm $,面积是 $ 10 cm^2 $,则斜边上的中线的长是
2.5
$ cm $.
答案:2.5
解析:
设直角三角形的斜边为$c$。
因为直角三角形面积$S = \frac{1}{2} × c × 4 = 10$,
所以$2c = 10$,解得$c = 5$。
又因为直角三角形斜边上的中线等于斜边的一半,
所以斜边上的中线长为$\frac{1}{2}c = \frac{5}{2} = 2.5$。
2.5
5. (2024·宿迁共同体期末)如图,在 $ Rt \triangle ABC $ 和 $ Rt \triangle ADB $ 中,$ \angle ADB = \angle ACB = 90° $,$ E $ 是 $ AB $ 的中点.
(1) 求证:$ DE = CE $;
(2) 若 $ \angle CAB = 30° $,$ \angle DBA = 40° $,求 $ \angle DEC $ 的度数.
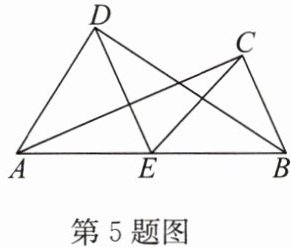
答案:
(1)证明:
∵∠ADB=∠ACB=90°,E是AB的中点,
∴DE=$\frac{1}{2}$AB,CE=$\frac{1}{2}$AB,
∴DE=CE.
(2)解:
∵CE=$\frac{1}{2}$AB=AE,DE=$\frac{1}{2}$AB=BE,
∴∠ECA=∠BAC=30°,∠EDB=∠DBA=40°.
∴∠AED=∠EDB+∠EBD=80°,∠BEC=∠ECA+∠EAC=60°.
∴∠DEC=180°−∠AED−∠BEC=40°.
6. (2024·宿豫期中)如图,在 $ \triangle ABC $ 中,点 $ D $,$ E $ 在 $ BC $ 上,$ AD \perp AB $,$ AE \perp AC $,且 $ BE = ED = DC $,则图中等腰三角形的个数为(
B
)
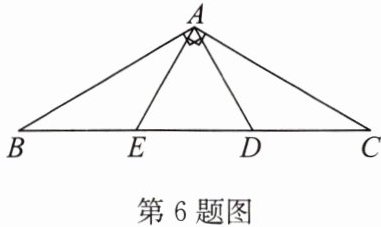
A.$ 3 $
B.$ 4 $
C.$ 5 $
D.$ 6 $
答案:B
解析:
证明:设 $ BE = ED = DC = x $,设 $ AB = c $,$ AC = b $,$ \angle BAD = \angle CAE = 90° $。
在 $ \triangle ABD $ 中,$ AD \perp AB $,设 $ AD = m $,则 $ BD = 2x $,由勾股定理得 $ AD^2 + AB^2 = BD^2 $,即 $ m^2 + c^2 = (2x)^2 $。
在 $ \triangle AEC $ 中,$ AE \perp AC $,设 $ AE = n $,则 $ EC = 2x $,同理 $ n^2 + b^2 = (2x)^2 $,故 $ m^2 + c^2 = n^2 + b^2 $。
设 $ \angle ADE = \alpha $,$ \angle AED = \beta $,在 $ \triangle ADE $ 中,由正弦定理得 $ \frac{AD}{\sin\beta} = \frac{AE}{\sin\alpha} = \frac{DE}{\sin\angle DAE} $。
易证 $ \triangle ABE \cong \triangle ACD $(SAS),得 $ AB = AC $,即 $ \triangle ABC $ 为等腰三角形。
由 $ BE = DE $,$ AB \perp AD $,可证 $ \triangle ABE $ 中 $ AE = BE $,同理 $ AD = DC $,$ AE = DE $,$ AD = DE $。
综上,等腰三角形有:$ \triangle ABC $、$ \triangle ABE $、$ \triangle ADC $、$ \triangle ADE $,共4个。
B