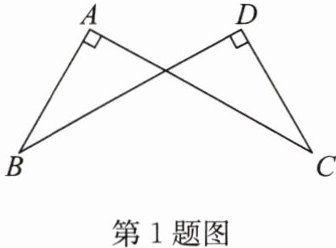
1. (2024·宿豫期末)如图,$\angle A= \angle D= 90^{\circ},AC= DB$. 求证:$AB= DC$.
答案:证明:如答图,连接BC;
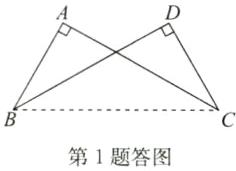
∵∠A=∠D=90°,
∴△ABC和△DCB都是直角三角形
在Rt△ABC和Rt△DCB中,$\left\{\begin{array}{l} BC=CB,\\ AC=DB,\end{array}\right. $
∴Rt△ABC≌Rt△DCB(HL),
∴AB=DC.
2. 如图,$AB= AE,\angle B= \angle E,BC= ED,AF$ 平分 $\angle BAE$,求证:$AF\perp CD$.
答案:证明:连接AC,AD.
在△ABC和△AED中,$\left\{\begin{array}{l} AB=AE,\\ ∠B=∠E,\\ BC=ED,\end{array}\right. $
∴△ABC≌△AED(SAS),
∴AC=AD,∠BAC=∠EAD.
∵AF平分∠BAE,
∴∠BAF=∠EAF,
∴∠BAF - ∠BAC=∠EAF - ∠EAD,
∴∠FAC=∠FAD.
在△ACF和△ADF中,$\left\{\begin{array}{l} AC=AD,\\ ∠FAC=∠FAD,\\ AF=AF,\end{array}\right. $
∴△ACF≌△ADF(SAS),
∴∠AFC=∠AFD.
∵∠AFC+∠AFD=180°,
∴∠AFC=90°,即AF⊥CD.
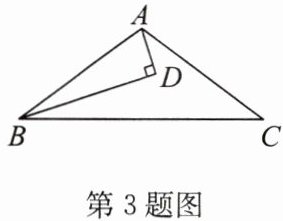
3. 如图,在 $\triangle ABC$ 中,$BD$ 平分 $\angle ABC,AD\perp BD,\angle CAD= \angle C$. 若 $AB= 5,AD= 2$,则 $BC$ 的长为(
D
)
A.6
B.7
C.8
D.9
答案:D
解析:
延长AD交BC于点E。
∵BD平分∠ABC,AD⊥BD,
∴∠ABD=∠EBD,∠ADB=∠EDB=90°。
在△ABD和△EBD中,
$\left\{\begin{array}{l} ∠ABD=∠EBD \\ BD=BD \\ ∠ADB=∠EDB\end{array}\right.$
∴△ABD≌△EBD(ASA)。
∴AD=DE=2,AB=BE=5。
∴AE=AD+DE=4。
∵∠CAD=∠C,
∴AE=CE=4。
∴BC=BE+CE=5+4=9。
答案:D
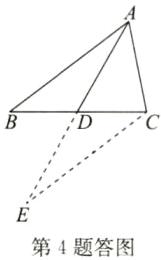
4. 如图,在 $\triangle ABC$ 中,$AD$ 为 $BC$ 边上的中线. 求证:$AB+AC>2AD$.
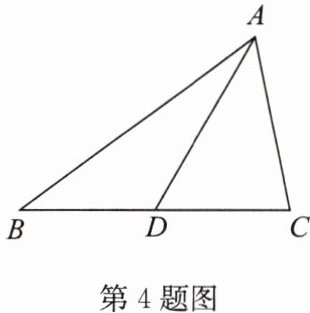
答案:证明:如答图,延长AD至点E,使DE=AD,连接CE.
∵AD为BC边上的中线,
∴BD=CD.
在△ABD和△ECD中,$\left\{\begin{array}{l} AD=ED,\\ ∠ADB=∠EDC,\\ BD=CD,\end{array}\right. $
∴△ABD≌△ECD,
∴AB=EC.
在△ACE中,
∵AC+EC>AE=2AD,
∴AB+AC>2AD.