1. 小亮不小心打碎了一块玻璃(如图),他根据所学的知识带了 $ B $ 部分去玻璃店配了一块完整的玻璃,他的依据是(
A
)
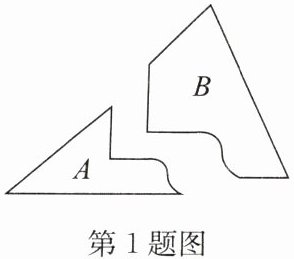
A.$ ASA $
B.$ SAS $
C.$ AAS $
D.$ SSS $
答案:A
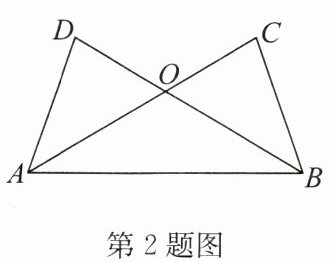
2. 如图,已知 $ AD = BC $,根据“$ SSS $”,还需要一个条件:
AC=BD
,可证明 $ \triangle ABC \cong \triangle BAD $;根据“$ SAS $”,还需要一个条件:
∠CBA=∠DAB
,可证明 $ \triangle ABC \cong \triangle BAD $.
答案:AC=BD ∠CBA=∠DAB
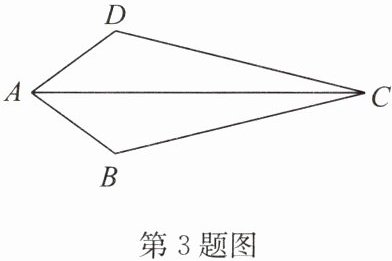
3. 如图,在 $ \triangle ABC $ 和 $ \triangle ADC $ 中,$ AB = AD $,$ BC = DC $,$ \angle B = 130^{\circ} $,则 $ \angle BAD + \angle BCD = $
100°
.
答案:100°
解析:
证明:在$\triangle ABC$和$\triangle ADC$中,
$\begin{cases}AB = AD \\BC = DC \\AC = AC\end{cases}$
$\therefore \triangle ABC \cong \triangle ADC$(SSS),
$\therefore \angle B = \angle D = 130°$,
在四边形$ABCD$中,$\angle BAD + \angle B + \angle BCD + \angle D = 360°$,
$\therefore \angle BAD + \angle BCD = 360° - \angle B - \angle D = 360° - 130° - 130° = 100°$。
$100°$
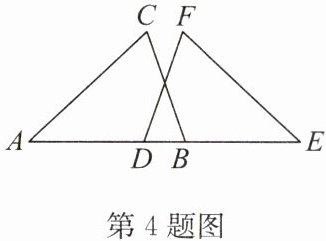
4. (2024·宿迁共同体期末)如图,点 $ A $,$ D $,$ B $,$ E $ 在同一直线上,$ AC = EF $,$ AD = BE $,$ BC = DF $. 求证:$ \angle ABC = \angle EDF $.
答案:证明:
∵AD=BE,
∴AD+DB=DB+BE,即AB=DE.又
∵AC=EF,BC=DF,
∴△ABC≌△EDF(SSS).
∴∠ABC=∠EDF.
5. 如图,在四边形 $ ABCD $ 中,$ AB = CD $,$ AD = BC $. 求证:$ \angle A = \angle C $.
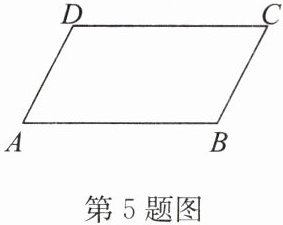
答案:证明:如答图,连接BD.
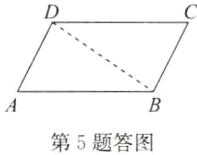
在△ABD和△CDB中,$\left\{\begin{array}{l} AB=CD,\\ AD=CB,\\ BD=DB,\end{array}\right. $
∴△ABD≌△CDB(SSS),
∴∠A=∠C.
6. 如图,在 $ \triangle ABC $ 和 $ \triangle DEF $ 中,已知 $ AB = DE $,$ BC = EF $. 在下列条件中,不能保证 $ \triangle ABC \cong \triangle DEF $ 的是(
B
)
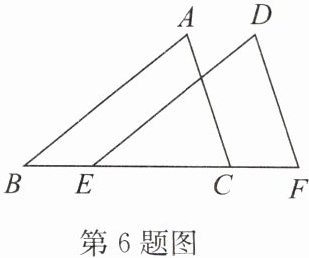
A.$ \angle B = \angle DEF $
B.$ \angle A = \angle D $
C.$ AB // DE $
D.$ AC = DF $
答案:B
解析:
要判定$\triangle ABC \cong \triangle DEF$,已知$AB = DE$,$BC = EF$。
选项A:若$\angle B = \angle DEF$,根据“SAS”(两边及其夹角对应相等的两个三角形全等),可证$\triangle ABC \cong \triangle DEF$。
选项B:若$\angle A = \angle D$,此时是“SSA”(两边及其中一边的对角对应相等),不能保证两个三角形全等。
选项C:若$AB // DE$,则$\angle B = \angle DEF$(两直线平行,同位角相等),结合$AB = DE$,$BC = EF$,由“SAS”可证$\triangle ABC \cong \triangle DEF$。
选项D:若$AC = DF$,根据“SSS”(三边对应相等的两个三角形全等),可证$\triangle ABC \cong \triangle DEF$。
综上,不能保证$\triangle ABC \cong \triangle DEF$的是选项B。
答案:B