13. (15分)(2024·广安)某小区物管中心计划采购A,B两种花卉用于美化环境.已知购买2株A种花卉和3株B种花卉共需要21元;购买4株A种花卉和5株B种花卉共需要37元.
(1)求A,B两种花卉的单价;
(2)该物管中心计划采购A,B两种花卉共计10000株,其中采购A种花卉的株数不超过B种花卉株数的4倍,当A,B两种花卉分别采购多少株时,总费用最少?并求出最少的总费用.
答案:解:
(1)设A种花卉的单价为x元,B种花卉的单价为y元.由题意得{2x+3y=21,4x+5y=37,解得{x=3,y=5.答:A种花卉的单价为3元,B种花卉的单价为5元.
(2)设采购A种花卉m株,则采购B种花卉(10000- m)株,总费用为W元.由题意得W=3m+5(10000-m)=-2m+50000.
∵m≤4(10000-m),解得m≤8000.在W=-2m+50000中,
∵-2<0,
∴W随m的增大而减小,
∴当m=8000时,W取得最小值,最小值为-2×8000+50000=34000,此时10000-m=2000.答:当采购A种花卉8000株,B种花卉2000株时,总费用最少,最少的总费用为34000元.
14. (15分)(2024·宿豫期末)如图,已知直线$l_{1}:y = x + 4与过点A(4,0)的直线l_{2}交于点B(\frac{4}{3},m)$,与$x$轴、$y轴分别交于点C$,$D$,直线$l_{2}交y轴于点E$.
(1)求直线$l_{2}$的函数表达式;
(2)若点$M在直线l_{1}$上,$MN// y$轴,交直线$l_{2}于点N$,且$MN = AC$,求点$M$的坐标;
(3)若点$P在直线l_{1}$上,以$P$,$D$,$E$为顶点的三角形为直角三角形,请写出点$P$的坐标.
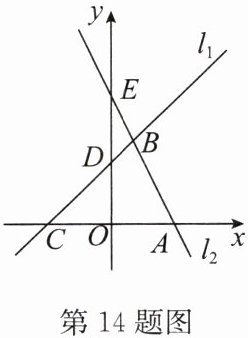
答案:解:
(1)在y=x+4中,当x=4/3时,y=4/3+4=16/3,
∴B(4/3,16/3).设直线l₂的函数表达式为y=kx+b,
∴{4/3k+b=16/3,4k+b=0,解得{k=-2,b=8.
∴直线l₂的函数表达式为y=-2x+8.
(2)在y=x+4中,当y=0时,x=-4,从而C(-4,0),AC=4-(-4)=8.设M(m,m+4),则N(m,-2m+8),
∴MN=|m+4-(-2m+8)|=|3m-4|.
∵MN=AC,
∴|3m-4|=8,
∴3m-4=8或3m-4=-8,
∴m=4或m=-4/3,
∴点M的坐标为(4,8)或(-4/3,8/3).
(3)在y=x+4中,当x=0时,y=4;在y=-2x+8中,当x=0时,y=8,
∴D(0,4),E(0,8).当∠PDE=90°时,PD⊥y轴,
∴点P的纵坐标为4,此时点P与点D重合,不符合题意;当∠PED=90°时,PE⊥y轴,
∴点P的纵坐标为8.在y=x+4中,当y=8时,x=4,此时点P的坐标为(4,8).当∠DPE=90°时,
∵OC=OD=4,
∴∠PDE=∠CDO=45°.
∴△PDE是等腰直角三角形,
∴PE=PD.
∴点P在线段DE的垂直平分线上.
∴点P的纵坐标为6.同理可得此时点P的坐标为(2,6).综上所述,点P的坐标为(4,8)或(2,6).