1. 在$\triangle ABC和\triangle A'B'C'$中,$AB = A'B'$,$\angle B = \angle B'$,补充条件后,仍不一定能保证$\triangle ABC \cong \triangle A'B'C'$,这个补充条件是(
D
)
A.$BC = B'C'$
B.$\angle C = \angle C'$
C.$\angle A = \angle A'$
D.$AC = A'C'$
答案:D
解析:
在$\triangle ABC$和$\triangle A'B'C'$中,已知$AB = A'B'$,$\angle B = \angle B'$。
选项A:补充$BC = B'C'$,根据“SAS”可判定$\triangle ABC \cong \triangle A'B'C'$。
选项B:补充$\angle C = \angle C'$,根据“AAS”可判定$\triangle ABC \cong \triangle A'B'C'$。
选项C:补充$\angle A = \angle A'$,根据“ASA”可判定$\triangle ABC \cong \triangle A'B'C'$。
选项D:补充$AC = A'C'$,属于“SSA”,不能保证$\triangle ABC \cong \triangle A'B'C'$。
D
2. 如图,已知$\angle ACB = \angle ACD$,要用“AAS”直接证明$\triangle ABC \cong \triangle ADC$,则需添加的一个条件是
∠B=∠D
.
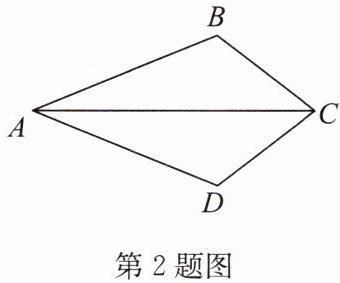
答案:∠B=∠D
3. 如图,在$\triangle ABC$中,已知$\angle 1 = \angle 2$,$BE = CD$,$AB = 5$,$AE = 2$,则$CE = $
3
.
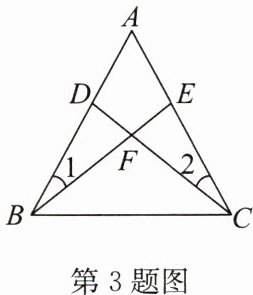
答案:3
解析:
证明:在$\triangle ABE$和$\triangle ACD$中,
$\angle A = \angle A$,
$\angle 1 = \angle 2$,
$BE = CD$,
$\therefore \triangle ABE \cong \triangle ACD(AAS)$,
$\therefore AD = AE = 2$,$AC = AB = 5$,
$\because AC = AE + CE$,
$\therefore CE = AC - AE = 5 - 2 = 3$。
3
4. 如图,在$\triangle ABC和\triangle DCB$中,$AC与BD交于点E$,$\angle A = \angle D$,$AB = DC$.
(1) 求证:$\triangle ABE \cong \triangle DCE$;
(2) 当$\angle AEB = 70^{\circ}$时,求$\angle EBC$的度数.
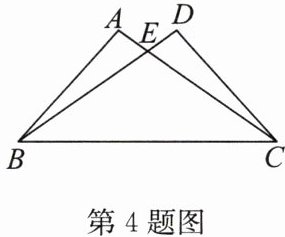
答案:
(1)证明:在△ABE和△DCE中,∠AEB=∠DEC,∠A=∠D,AB=DC,
∴△ABE≌△DCE(AAS).
(2)解:
∵△ABE≌△DCE,
∴EB=EC,
∴△EBC是等腰三角形,
∴∠EBC=∠ECB.
∵∠AEB=70°=∠EBC+∠ECB,
∴∠EBC=35°.
5. 在$\triangle ABC$中,$\angle A = 60^{\circ}$,$\angle B = 50^{\circ}$,$AB = 8$,下列条件能得到$\triangle ABC \cong \triangle DEF$的是(
C
)
A.$\angle D = 60^{\circ}$,$\angle E = 50^{\circ}$,$DF = 8$
B.$\angle D = 60^{\circ}$,$\angle F = 50^{\circ}$,$DE = 8$
C.$\angle E = 50^{\circ}$,$\angle F = 70^{\circ}$,$DE = 8$
D.$\angle D = 60^{\circ}$,$\angle F = 70^{\circ}$,$EF = 8$
答案:C
解析:
在$\triangle ABC$中,$\angle A=60°$,$\angle B=50°$,则$\angle C=180° - 60° - 50°=70°$,$AB=8$。
选项A:$\angle D=60°$,$\angle E=50°$,则$\angle F=70°$,但$DF$对应$\triangle ABC$中的边不确定,无法判定全等。
选项B:$\angle D=60°$,$\angle F=50°$,则$\angle E=70°$,$DE=8$,此时$DE$对应$\triangle ABC$中的$AC$,非已知边$AB$,无法判定全等。
选项C:$\angle E=50°$,$\angle F=70°$,则$\angle D=60°$,$DE=8$,此时$\angle D=\angle A=60°$,$\angle E=\angle B=50°$,$DE=AB=8$,符合“ASA”全等判定条件,能判定$\triangle ABC\cong\triangle DEF$。
选项D:$\angle D=60°$,$\angle F=70°$,则$\angle E=50°$,$EF=8$,$EF$对应$\triangle ABC$中的$BC$,非已知边$AB$,无法判定全等。
C
6. (2024·牡丹江)如图,$\triangle ABC$中,$D是AB$上一点,$CF // AB$,$D$,$E$,$F$三点共线,请添加一个条件:
DE=EF
,使得$AE = CE$.(只添一种情况即可)
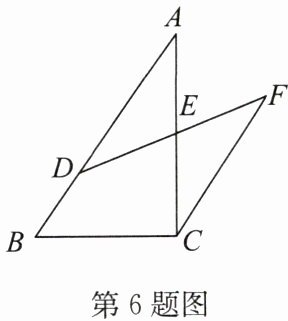
答案:DE=EF(答案不唯一)
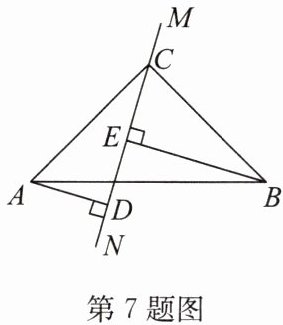
7. 如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = BC$,直线$MN经过点C$,且$AD \perp MN$,$BE \perp MN$,垂足分别是$D$,$E$,则$AD$,$DE$,$BE$之间的数量关系是
AD+DE=BE
.
答案:AD+DE=BE
解析:
证明:
∵∠ACB=90°,AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,∠ACD+∠BCE=90°,∠ACD+∠CAD=90°,
∴∠CAD=∠BCE。
在△ADC和△CEB中,
$\left\{\begin{array}{l} ∠ADC=∠CEB \\ ∠CAD=∠BCE \\ AC=BC \end{array}\right.$,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE。
∵CD=CE+DE,
∴BE=AD+DE。
AD+DE=BE