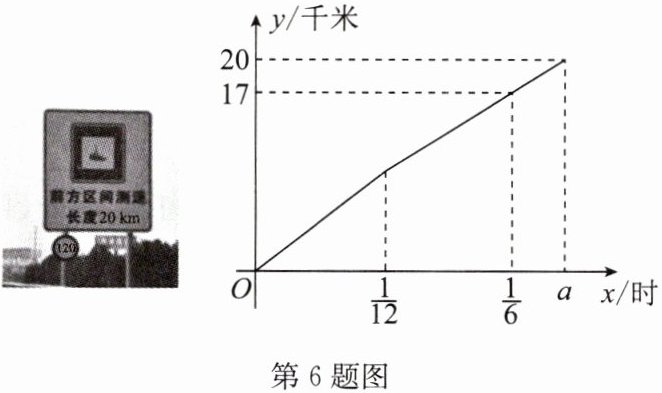
6. (2024·长春) 区间测速是指在某一路段前后设置两个监控点,根据车辆通过两个监控点的时间来计算车辆在该路段上的平均行驶速度. 小春驾驶一辆小型汽车在高速公路上行驶,其间经过一段长度为 20 千米的区间测速路段,从该路段起点开始,他先匀速行驶 $ \frac{1}{12} $ 小时,再立即减速以另一速度匀速行驶 (减速时间忽略不计),当他到达该路段终点时,测速装置测得该辆汽车在整个路段行驶的平均速度为 100 千米/时. 汽车在区间测速路段行驶的路程 $ y $(千米) 与在此路段行驶的时间 $ x $(时) 之间的函数图象如图所示.
(1) $ a $ 的值为
$\frac{1}{5}$
;
(2) 当 $ \frac{1}{12} \leq x \leq a $ 时,求 $ y $ 与 $ x $ 之间的函数表达式;
解:设当$\frac{1}{12}\leqslant x\leqslant \frac{1}{5}$时,y 与 x 之间的函数表达式为$y=kx+b(k\neq 0)$,
则$\left\{\begin{array}{l}\frac{1}{12}k+b=9.5,\\ \frac{1}{5}k+b=20,\end{array}\right.$解得$\left\{\begin{array}{l}k=90,\\ b=2,\end{array}\right.$
$\therefore y=90x+2\left(\frac{1}{12}\leqslant x\leqslant \frac{1}{5}\right)$.
(3) 通过计算说明在此区间测速路段内,该辆汽车减速前是否超速. (此路段要求小型汽车行驶速度不得超过 120 千米/时)
解:当$x=\frac{1}{12}$时,$y=90× \frac{1}{12}+2=9.5$,
$\therefore$先匀速行驶$\frac{1}{12}$小时的速度为$9.5÷ \frac{1}{12}=114$(千米/时).
$\because 114<120$,$\therefore$该辆汽车减速前没有超速.
答案:
(1)$\frac{1}{5}$
(2)解:设当$\frac{1}{12}\leqslant x\leqslant \frac{1}{5}$时,y 与 x 之间的函数表达式为$y=kx+b(k\neq 0)$,
则$\left\{\begin{array}{l}\frac{1}{6}k+b=17,\\ \frac{1}{5}k+b=20,\end{array}\right.$解得$\left\{\begin{array}{l}k=90,\\ b=2,\end{array}\right.$
$\therefore y=90x+2\left(\frac{1}{12}\leqslant x\leqslant \frac{1}{5}\right)$.
(3)解:当$x=\frac{1}{12}$时,$y=90× \frac{1}{12}+2=9.5$,
$\therefore$先匀速行驶$\frac{1}{12}$小时的速度为$9.5÷ \frac{1}{12}=114$(千米/时).
$\because 114<120$,$\therefore$该辆汽车减速前没有超速.
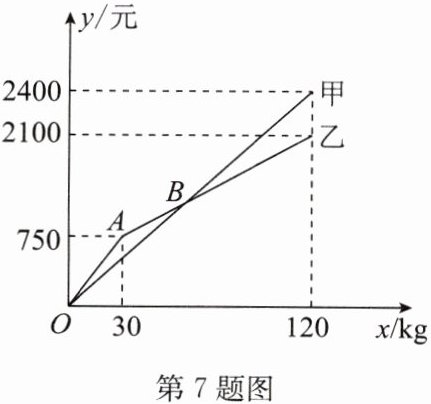
7. 某水果店购进甲、乙两种苹果的进价分别为 8 元/kg、12 元/kg,这两种苹果的销售额 $ y $(元) 与销售量 $ x $(kg) 之间的关系如图所示.
(1) 求甲种苹果的销售额 $ y $ 与销售量 $ x $ 之间的函数关系式;
(2) 求点 $ B $ 的坐标,并写出点 $ B $ 表示的实际意义;
(3) 若不计损耗等因素,当甲、乙两种苹果的销售量均为 $ a $($ a > 30 $) kg 时,它们的利润和为 1650 元,求 $ a $ 的值.
答案:解:
(1)设甲种苹果的销售额 y 与销售量 x 之间的函数关系式是$y=kx$.
$\because$点$(120,2400)$在该函数的图象上,$\therefore 2400=120k$,
解得$k=20$,
即甲种苹果的销售额 y 与销售量 x 之间的函数关系式是$y=20x$.
(2)当$30\leqslant x\leqslant 120$时,设乙种苹果图象对应的函数表达式为$y=mx+n$.
$\because$点$(30,750)$,$(120,2100)$在该函数的图象上,
$\therefore \left\{\begin{array}{l}30m+n=750,\\ 120m+n=2100,\end{array}\right.$解得$\left\{\begin{array}{l}m=15,\\ n=300,\end{array}\right.$
即当$30\leqslant x\leqslant 120$时,乙种苹果图象对应的函数表达式为$y=15x+300$,
由$\left\{\begin{array}{l}y=20x,\\ y=15x+300,\end{array}\right.$可得$\left\{\begin{array}{l}x=60,\\ y=1200,\end{array}\right.$
即点 B 的坐标为$(60,1200)$,点 B 表示的实际意义是当销售量为 60 kg 时,甲和乙两种苹果的销售额相同,都是 1200 元.
(3)由题图可得,
甲种苹果的销售单价为$2400÷ 120=20$(元).
当$x\leqslant 30$时,乙种苹果的销售单价为$750÷ 30=25$(元);
当$x>30$时,乙种苹果的销售单价为$(2100-750)÷ (120-30)=15$(元).
由题意,可得$(20-8)a+(25-12)× 30+(15-12)(a-30)=1650$,
解得$a=90$,即 a 的值为 90.