1. (2024·陕西)如图,在△ABC中,∠BAC= 90°,AD是BC边上的高,E是BC边的中点,连接AE,则图中的直角三角形共有 (
C
)
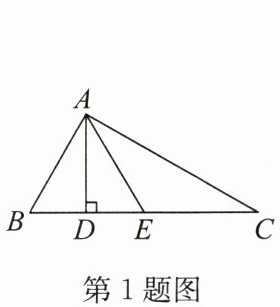
A.2个
B.3个
C.4个
D.5个
答案:C
2. (2024·宿豫期中)下列各组线段能搭成一个三角形的是 (
B
)
A.2 cm,2 cm,4 cm
B.5 cm,4 cm,3 cm
C.1 cm,2 cm,3 cm
D.2 cm,3 cm,7 cm
答案:B
解析:
根据三角形三边关系:任意两边之和大于第三边。
A. $2 + 2 = 4$,不满足,不能搭成三角形。
B. $3 + 4 > 5$,$3 + 5 > 4$,$4 + 5 > 3$,满足,能搭成三角形。
C. $1 + 2 = 3$,不满足,不能搭成三角形。
D. $2 + 3 < 7$,不满足,不能搭成三角形。
B
3. 如图,图中以BC为边的三角形的个数为
4
.
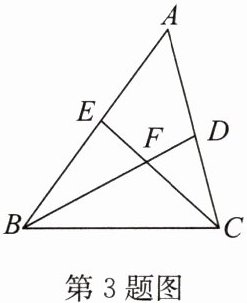
答案:4
解析:
以BC为边的三角形有:△ABC,△BEC,△BDC,△BFC。
个数为4。
4. 把12 cm长的铁丝截成三段,每段长度均为整数. 若将这三段铁丝首尾顺次相接组成三角形,则不同的三角形有
3
种.
答案:3
解析:
设三段铁丝长度分别为$a\ cm$、$b\ cm$、$c\ cm$,且$a \leq b \leq c$,$a$、$b$、$c$为正整数。
由题意得$a + b + c = 12$,根据三角形三边关系$a + b > c$,则$c < 6$。又因为$c \geq \frac{12}{3} = 4$,所以$c$可取$4$、$5$。
当$c = 4$时,$a + b = 8$,且$a \leq b \leq 4$,则$b = 4$,$a = 4$,即$(4, 4, 4)$。
当$c = 5$时,$a + b = 7$,且$a \leq b \leq 5$,则$b$可取$5$、$4$,对应$a = 2$、$3$,即$(2, 5, 5)$、$(3, 4, 5)$。
综上,不同的三角形有$3$种。
3
5. 一个等腰三角形的周长是85 cm.
(1)若腰长是底边长的2倍,求腰长;
(2)已知其中一边长为20 cm,求其他两边的长.
答案:解:
(1)设底边长为x cm,则腰长为2x cm. 根据题意,得x+2x+2x=85,解得x=17,故腰长为2x=2×17=34(cm).
(2)因为长为20 cm的边可能是腰,也可能是底边,所以分两种情况: 当长为20 cm的边为腰时,底边长为85-20×2=45(cm),而20+20<45,即两边之和小于第三边,所以20 cm长的边为腰不能组成三角形,舍去; 当长为20 cm的边为底边时,腰长为(85-20)÷2=32.5(cm),而20 cm,32.5 cm,32.5 cm可以组成三角形,故三角形其他两边的长都为32.5 cm.
6. 已知a,b,c分别为△ABC中∠A,∠B,∠C的对边长,化简:|a+b-c|+|b-c-a|-|c-a+b|.
答案:解:因为a,b,c分别为△ABC中∠A,∠B,∠C的对边长,所以a+b-c>0,b-c-a<0,c-a+b>0, 所以|a+b-c|+|b-c-a|-|c-a+b|=a+b-c-b+c+a-c+a-b=3a-b-c.
解析:
解:因为$a,b,c$分别为$\triangle ABC$中$\angle A,\angle B,\angle C$的对边长,所以$a+b-c>0$,$b-c-a<0$,$c-a+b>0$.
所以$|a+b-c|+|b-c-a|-|c-a+b|=(a+b-c)+(-b+c+a)-(c-a+b)$
$=a+b-c -b +c +a -c +a -b$
$=3a -b -c$.